3.4. Характеристика рядів розподілу Ряди розподілу характеризуються коефіцієнтом асиметрії та коефіцієнтом ексцесу.

Коефіцієнт асиметрії показує скошеність кривої нормального закону розподілу вправо чи вліво відносно осі ОХ.

де 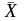‑ середнє значення ознаки;

Ме - медіана ознаки;

 ‑ середньоквадратичне відхилення.

Якщо А0, то скошеність буде лівостороння.

Якщо А0, то скошеність буде правосторонньою.

Якщо А=0 – розподіл симетричний.

Для нормального розподілу характерним є те, що середня арифметична, мода і медіана рівні між собою

Коефіцієнт ексцесу характеризує гостровершність вершини розподілу, скупченість варіантів навколо середньої арифметичної.

де  ‑ середньоквадратичне відхилення;

 ‑ центральний момент розподілу.

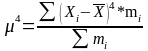
де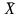 ‑ середнє значення ознаки;

Xi – індивідуальне значення ознаки;

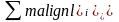- загальна сума частот усіх інтервалів.

Якщо Е3, то вершина кривої розподілу – гостроверха.

Якщо Е3 – нормальна крива.

Якщо Е3 ‑ вершина кривої розподілу – тупа вершина.

1. Виконаємо розрахунки для віку працівників:

А=( 37–34,5)/10,3=0,24 – крива розподілу працівників за віком скошена вправо (А>0).

Розрахуємо спочатку центральний момент розподілу:

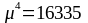
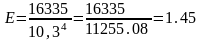
_{Таким чином, маємо тупу вершину розподілу працівників за віком, оскільки Е<3.}

Рис.6. Розподіл працівників за віком.

1. Виконаємо розрахунки для відпрацьованого часу :

А=( 60,69 - 60,4)/4,1 = 0,05– крива розподілу працівників за відпрацьованим часом скошена вправо (А>0).

_{Вершина розподілу працівників за відпрацьованим часом – тупа, бо Е<3.}

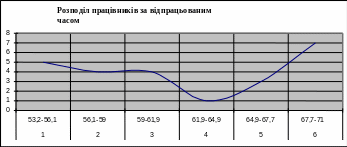
Рис.7. Розподіл працівників за відпрацьованим часом .

1. Виконаємо розрахунки для коефіцієнту використаного робочого дня :

А=( 1,17 – 1,21)/0,3 = -0.13-- крива розподілу працівників за коефіцієнтом використаного робочого дня скошена вліво (А<0).

Проведемо розрахунки коефіцієнта ексцесу.

_{Вершина розподілу працівників за коефіцієнтом використання робочого дня – тупа , оскільки Е<3.}

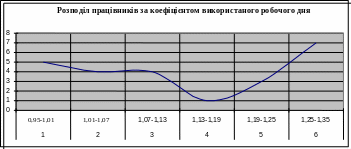
Рис.8. Розподіл працівників за коефіцієнтом використаного робочого дня.

3.5. Перенесення результатів вибіркового спостереження на генеральну сукупність.

Вибіркове спостереження відрізняється від інших несуцільних такими ознаками:

1. Ще до проведення визначається, яка кількість одиниць сукупності буде обстежена.

2. Визначається яким способом будуть відбиратися одиниці з генеральної сукупності в вибіркову.

Переваги вибіркового спостереження:

1. Економія часу і ресурсів.

2. Зведення до мінімуму руйнування одиниці сукупності.

3. Коли необхідно детально обстежити одиниці сукупності, що неможливо зробити по всій сукупності.

Головними задачами вибіркового спостереження є:

1. Визначення граничної помилки репрезентативності для різних способів відбору.

2. Визначення необхідного об’єму вибірки, який забезпечить певний рівень помилки репрезентативності.

В даному випадку маємо без повторний власне випадковий відбір. Для цього способу середня помилка репрезентативності становить:

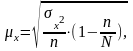
де ² – дисперсія, квадрат середньоквадратичного відхилення;

n – кількість одиниці вибіркової сукупності;

N ‑ кількість одиниці генеральної сукупності.

Гранична помилка репрезентативності (залежить від коефіцієнту довіри t):

_х = t×_х,

де t = 1, при ймовірності 0,683;

t = 2,при ймовірності 0,954;

t = 3, що відповідає ймовірності 0,997.

Розповсюдження результатів безповторного вибіркового спостереження на генеральну сукупність здійснюється методом прямого перерахування, коли узагальнюючий показник вибіркової сукупності множиться на кількість одиниць генеральної сукупності.

Проведемо розрахунки помилок репрезентативності для кожної ознаки, що розглядаються в ході спостереження. Приймемо заданий коефіцієнт довіри t = 2 при ймовірності 0,954.

1. Для віку працівників:

Середня помилка репрезентативності:

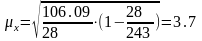
Гранична помилка репрезентативності:

_х = 3,7*2=7.4

З урахуванням заданої вірогідності спостереження (95,4%), можна сказати, що середнє значення віку працівників знаходиться в межах:

29.6 <віку працівників< 44.4

2. Для відпрацьованого часу:

Середня помилка репрезентативності:

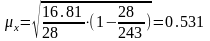
Гранична помилка репрезентативності:

_х = 0,531*2=1,062 (год /в день)

З урахуванням заданої вірогідності спостереження (95,4%), можна сказати, що середнє значення відпрацьованого часу знаходиться в межах:

59.628 год/в день < відпрацьований час < 61.752 год/в день.

3. Для коефіцієнта використаного робочого дня:

Середня помилка репрезентативності:

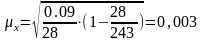
Гранична помилка репрезентативності:

_х = 0,003*2=0,006(/год)

З урахуванням заданої вірогідності спостереження (95,4%), можна сказати, що середнє значення коефіцієнта використаного робочого дня знаходиться в межах:

1.164 год< коефіцієнта використаного робочого дня< 1.176 год.