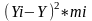3.6.2. Визначення взаємозв’язків між факторними та результативними ознаками

Існують такі види зв’язку:

- функціональний – кожному значенню факторної ознаки відповідає одне - значення результативної ознаки.

- стохастичний - кожному значенню факторної ознаки відповідає множина значень результативної, які утворюють умовний розподіл.

Існує декілька методів виявлення зв’язка між двома ознаками:

- метод аналітичних групувань;

- метод регресії і кореляції;

- метод кореляції рангів.

В даній частині курсової роботи буде виявлений зв’язок між кількістю їздок та виручкою за допомогою методу аналітичних групувань і методу регресії та кореляції.

Вимірювання зв’язку методом аналітичних групувань, який складається з таких етапів:

1. побудова аналітичного групування;

2. оцінка лінії регресії—тут оцінюють еластичність : чи реагує результативна ознака на зміну факторної.

3. визначення щільності зв’язку між факторною та результативною ознакою за формулою:

,

де 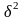-міжгрупова дисперсія,

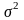- загальна дисперсія.

Для обчислення міжгрупової дисперсії використаємо формулу:

,

де - середнє значення ознаки по всій сукупності;

- середнє значення ознаки для кожної з груп;

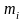- частоти.

4. Перевірка істотності зв’язку—це порівняння фактичного значення щільності зв’язку з його критичним значенням, яке ми беремо з таблиці даних. Фактичне значення розраховуємо за формулою:

F_ф де Κ₁ = Г – 1 К₂ = n – Г

Якщо F_кр ≤ F_ф, то зв'язок істотний.

Цей метод добре застосовувати для великих сукупностей.

Визначимо зв'язок між віком і відпрацьованим часом.

Побудуємо аналітичне групування залежності відпрацьованим часом від віку, також в таблицю додамо стовпці для обчислення між групової дисперсії.

Таблиця 3.7.

Залежність відпрацьованого часу від віку

№ п\п	Вік	Кіль-кість працівників	Загальній відпрацьований час	Cередній відпрацьований час	Yi-Y
1	21-26,2	8	499.9	62.4	1.71	2.9241	23.3928
2	26,2-31,4	3	183	61	0.31	0.0961	0.2883
3	31,4-36,6	5	295.4	59.08	-1.61	2.5921	12. 9605
4	36,6-41,8	2	112.3	56.15	-4.54	20.6116	41.2232
5	41,8-47	3	125.15	41.72	-18.97	359.8609	1079.5827
6	47-52	7	419	59.86	-0.83	0.6889	4.8223

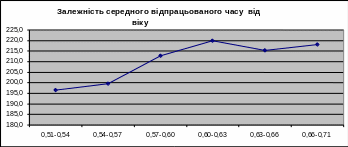Рис.10. Залежність відпрацьованого часу від віку.

Визначимо щільність зв’язку між віком і відпрацьованим часом.

-- таким чином маємо слабкий зв'язокміж віком і відпрацьованим часом, оскільки .

Перевіримо істотність зв’язку:

К₁= 6 - 1 = 5 ,

К₂= 28 - 6=22

F_ф= 0.71 /(1- 0.71 )*22/ 5=10.78

F_кр=2,67

В даному випадку F_кр < F_ф, отже зв'язок між віком і відпрацьованим часом, вважається, що він спричинений випадковими факторами.

Іншим методом визначення взаємозв’язків між факторною і результативною ознакою метод регресії і кореляції.

На першому етапі при застосуванні цього методу визначають рівняння регресії. Задача регресійно-кореляційного методу полягає у виявленні зв’язку між факторною та результативною ознаками, та виборі рівняння регресії методом найменших квадратів. Це означає, що сума різниць квадратів теоретичних і емпіричних значень повинна бути мінімальною.

(У_і - У)² min

На наступному етапі необхідно знайти параметри рівняння:

У = а + b*х

де а – параметр, що показує значення результативної ознаки (у), якщо факторна ознака х = 0;

b – параметр, що показує на скільки одиниці змінюється у середньому результативна ознака (у), якщо факторну ознаку змінити на одиницю.

Д ля знаходження параметрів будується система рівняння:

n*a + b* x =  y

a* x + b* x² =  x*y

Для розв’язку системи рівнянь побудуємо допоміжну таблицю.

На наступному етапі проводиться оцінка щільності зв’язку. Щоб виявити щільність зв’язку, вимірюють лінійний коефіцієнт кореляції Пірсона:

Лінійний коефіцієнт кореляції r змінюється в межах - 1  r  +1. Він показує напрямок і тісноту зв’язку між ознаками.

На заключному етапі перевіряється істотність зв’язку.

_{Fф ,}

де Κ₁ = c– 1 К₂ = n – c, с—кількість коефіцієнтів в рівнянні регресії.

Розглянемо взаємозв’язок між технічною швидкістю (факторна ознака) і продуктивністю праці (результативна ознака).

Побудуємо кореляційне поле.

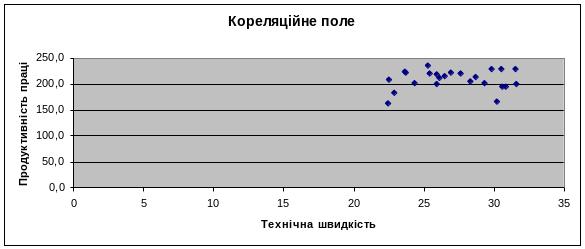
Рис. 11.Кореляційне поле.

Припускаємо, залежність лінійна. Побудуємо допоміжну таблицю.

Таблиця 3.8.

Зв'язок між коефіцієнта використаного робочого дня (факторна ознака) і відпрацьованим часом (результативна ознака).

№ п\п	Коефіцієнт використаного робочого дня	Відпрацьований час	X^2	XY	Y(теор)
1	1,30	65,3	1,69	84,89	120,4
2	1,03	71	1,0609	73,13	107,63
3	0,95	53,5	0,9025	50,8	103,84
4	0,99	57,9	0,9801	57,321	105,73
5	0,96	63	0,9216	60,48	104,31
6	1,05	60,2	1,1025	65,1	108,57
7	1,32	57,3	1,7424	75,636	121,34
8	1,33	58,5	1,7689	77,805	121,82
9	1,25	62,1	1,5625	77,625	118,03
10	1,99	59,1	3,9601	117,609	153,03
11	1,24	55,6	1,5376	68,944	117,56
12	1,15	56	1,3225	64,4	113,3
13	1,09	58	1,1881	63,22	110,46
14	1,35	63,2	1,8225	85,32	122,76
15	1,24	66	1,5376	81,84	117,56
16	1,12	61,4	1,2544	68,768	111,88
17	1,33	62,7	1,7689	90,041	121,82
18	0,97	57,5	0,9409	55,775	104,79
19	0,95	64,3	0,9025	61,085	103,84
20	1,35	58,5	1,8225	78,975	122,76
21	1,22	59,7	1,4884	72,834	116,61
22	1,32	53,2	1,7424	70,224	121,34
23	1,20	63,8	1,44	76,56	115,67
24	1,25	66	1,5625	82,5	118,03
25	1,25	66,1	1,5625	82,625	118,03
26	1,32	57,7	1,7424	76,164	121,34
27	1,35	60,5	1,8225	81,675	122,76
28	1,33	61,2	1,7689	81,396	121,82
	28,97	1699,3	42,919	2082,7
	1,0346	774,97	1,532	74,382

З системи рівнянь отримуємо рівняння регресії:

28а+ 1.034b=1698

1.034a+ 42.919b=2082.7

а=58,906

b=47,301

Функція має вигляд:

Y= 58,906 + 47,301х.

Відповідно до функції розрахуємо теоретичні значення результативної ознаки. Ці значення наведено в останньому стовпці табл. 3.13.

За допомогою коефіцієнта кореляції Пірсона оцінимо щільність зв’язку між віком і відпрацьованим часом.

XY=74,382

X=1,0346

Y=774,97

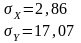
Отже, коефіцієнт кореляції має значення:

r =( 74,382- 1,0346*774,97 )/( * )=+ ,

тому можна зробити висновок, що зв'язок є досить суттєвим, оскільки значення коефіцієнта кореляції є досить близьким до 1.

Перевіримо істотність зв’язку між залишковою вартістю і кількістю їздок.

К₁= 2 - 1=1

К₂= 28- 2 =26

F_ф= / *26/1=

F_кр=4,22

Таким чином, F_кр F_ф, що вказує на неістотність зв’язку між віком і відпрацьованим часом.