9

МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(Технический университет)

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ПРАКТИЧЕСКИМ РАБОТАМ

по курсу «Материалы электронных средств»

Москва, 2012 г.

I. Цель выполнения практических работ.

Цель работ - знакомство со свойствами твердых тел, используемых для реализации современных микроэлектронных приборов и овладение методами их автоматизированного расчета с использование пакета математических программ MathCad.

II. Задания.

(M01-03)

Задание М-1. Расчет относительной электроотрицательности в молекулах

H Br, H I, H Cl, H F.

Как известно, при образовании ковалентной связи между атомами разных элементов общее электронное облако смещается к элементу с большей электроотрицательностью c. Относительная электроотрицательность:

Dc = c ₁ - c₂.

Асимметрия приводит к увеличению дипольного момента молекулы M и, следовательно, к усилению связи между молекулами и увеличению прочностных характеристик материалов.

1. Преобразовать данные в форму, удобную для расчета с помощью программы MathCad. (Первая компонента всех молекул – Н, поэтому целесообразно придать значение этого аргумента в виде константы. Величина второй компоненты изменяется, поэжтому аргумент может быть представлен в виде табличной переменной с подстрочным индексом. См. Приложение М-1.1.)

2. Рассчитать относительную электроотрицательность Dc с помощью программы MathCad.

3. По результатам расчета заполнить таблицу в порядке возрастания относительной электроотрицательности Dc.

Таблица М-1.1.

Молекула	Dc

4. Нарисовать эскизы для каждой из молекул, на которых отметить расположение элементов относительно условного центра (условный центр соответствует результирующему положительному заряду). Из эскизов и вывода к работе должно быть понятно, какая из молекул обладает большим дипольным моментом М. Это будет выводом к работе.

_______________________

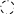H -

В отчете представить заполненную таблицу М-1, эскизы.

Справочные данные:

Таблица М-1.2.

Значения электротрицательности χ химических элементов.

H 2.1
Li 0.98	Be 1.5	B 2.0	C 2.5	N 3.07	O 3.5	F 4.0
Na 0.93	Mg 1.2	Al 1.6	Si 1.9	P 2.2	S 2.6	Cl 3.0
K 0.91	Ca 1.04	Ga 1.8	Ge 2.0	As 2.1	Se 2.5	Br 2.8
Rb (рубидий) 0.89	Sr (стронций) 0.99	In (индий) 1.5	Sn (олово) 1.7	Sb (сурьма) 1.8	Te (теллур) 2.1	I (иод) 2.6

Приложение М-1.1.

Язык программы MathCad: EN. Доли целого числа отделяются точкой (7.2).

Идентификаторы – имена аргументов и функций – обозначаются сочетанием одной или нескольких строчных латинских или греческих букв (больших или маленьких) и цифр.

Практично при наборе знаков использовать возможности дополнительных панелей инструментов.

Последовательность формирования задания для расчетов (вместо знака равенства «=» вводится знак присвоения «:=»):

- определение аргумента – константы (например, b:= 2.1),

- определение аргументов - переменных (диапазонных или в виде таблицы),

- формирование диапазона (на панели инструментов «m..n») подстрочных индексов, начиная с 0-ого (например, i:=0..3),

- таблица ввода переменной с подстрочным индексом формируется после ввода первого числа и запятой «,» (например, c_i:== 7.2,),

- запись функции (например, a_i:= b - c_i).

Результаты расчетов представляются после набора a_i и нажатия клавиши «=».

Задание м-3. Анализ геометрии кристаллической решетки с помощью функции Polyhedron программы MathCad.

Функция Polyhedron строит многогранник из своей коллекции под номером, например, # 11 - куб.

- На пустом месте рабочего листа щелкните мышью.

- Нажмите комбинацию клавиш Ctrl + 2 . На месте красного креста появится шаблон графика.

- Введите в метке шаблона строчку (string) Polyhedron(“#11”).

- Щелкните мышью вне области графика. Появиться трехмерный график многогранника.

- Водя мышью с нажатой левой клавишей по полю графика, можно наблюдать многогранник с разных сторон.

В отчете отметить номера и соответствующие им многогранники.

Задание М-5. Расчет тензорезистивного датчика.

Тензорезисторы используются для датчиков давления, веса, ускорения, деформации. Работа тензометрических весов основана на измерении стрелы прогиба центра балки, лежащей на опорах.

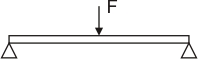
Рис.М-5.1. Эскиз измерительной балки.

Если на нижнюю сторону балки прямоугольного сечения наклеить тензорезистор, то относительная деформация резистора будет:

ε = 3 F L / (2 E a b²),

где F – приложенная сила в середине балки, L – длина балки, поперечное сечение балки имеет форму прямоугольника с шириной a и толщиной b, Е – модуль Юнга материала балки из таблицы М-5.1.

Тензорезистор изготавливается из материала, сопротивление R которого заметно меняется при деформации ε. Такими материалами могут быть металлические сплавы или полупроводники.

Металлические тензорезисторы представляют собой проволоку диаметром 0.02 – 0.005 мм или фольгу толщиной 3 мкм, уложенные меандром на полиимидной (или аналогичной тонкой) пленке. Благодаря пластичности сплавы при деформации практически не изменяют своего удельного сопротивления ρ. Изменение сопротивления R происходит за счет изменения длины l и, вследствие эффекта Пуассона, размеров поперечного сечения S тензорезистора.

R = ρ l / S, (Δ R = ρ Δl / Δ S)

ρ – удельное сопротивление материала тензорезистора, l – длина и S – площадь поперечного сечения тензорезистора. Для получения заметного эффекта необходима большая длина l резистора вдоль действия силы вдоль направления деформации.

Полупроводниковые тензорезисторы представляют собой легированный полупроводник площадью от 50 х 50 мкм до 1 х 1 мм. Внутренние напряжения, создаваемые легирующей примесью, являются причиной значительных изменений удельного сопротивления ρ даже при небольших деформациях. Следовательно, изменение сопротивления R полупроводниковых тензорезисторов происходит в результате изменения ρ.

Оказалось удобнее оценивать относительное изменение сопротивления тензорезистора с помощью коэффициента пропорциональности между механической деформацией и изменение электрического сопротивления - коэффициента К тензочувствительности измерительного резистора R_изм:

R_изм/(R₁ + R_изм) = K· ε.

При измерении сопротивления тензорезистора R_изм используют полумостовую схему подключения (рис.М-5.2). От ЦАП подается напряжение питания моста, которое измеряется входом 2 АЦП. Изменение напряжения на измерительном тензорезисторе фиксируется на входе 1 АЦ П. В качестве базового сопротивления R₁ обычно используется такой же тензорезистор, как и измерительный, только наклеенный на балку в перпендикулярном направлении, нечувствительном к деформации. Это упрощает термокомпенсацию схемы (тензорезисторы обладают высоким температурным коэффициентом сопротивления, поскольку изменение температуры).

Рис.М-5.2 Структурная полумостовая схема включения тензорезисторов.

Рис. Тензодатчик механических деформаций металлической трубы.

1. Сформировать в виде графика калибровочные кривые силометра (относительное изменение сопротивление R тензорезистора в зависимости от действующей силы F в диапазоне от 10 до 1000 Н)

для различных материалов балки с размерами a =10 мм, b = 8 мм, l = 10 см,

для различных типов тензорезисторов металлических и полупроводниковых.

2. В отчете привести калибровочные кривые и ответы на вопросы коротко с поясняющими эскизами.

Вопросы:

1) Как надо разместить измерительный и базовый резисторы на а) круглой мембране и б) консольной балке? (Опора препятствует сдвигу, а свободный конец консольной балки снимает внутренние напряжения)

2) Предложите топологию металлического тензорезистора для размещения на плоскости с неизвестным направлением деформации.

3) Какие бы Вы дали рекомендации по применению материалов тензорезисторов в зависимости от размеров и формы объекта измерения? (Критерии точности, экономичности и т.п.).

Справочные данные.

Таблица М-5.1.

Материал балки	Модуль Юнга, 109 Н/м2
Сталь	196
Латунь	102
Алюминий	68

Таблица М-5. 2.

Материал тензорезистора	Коэффициент К тензочувствительности
Проволока из сплава Константан: Ni – 45%, Cu – 55%	2.1
Проволока из платино - вольфрамового сплава: Pt – 92%, W – 8%	4.1
Полупроводник на основе саммария Sm S	75

Приложение М-5.1.

MathCad.

Определить константы.

Переменные аргументы представить в виде таблиц ввода, а сами аргументы – с подстрочными индексами.

Для формирования графических зависимостей необходимо переменную задать в виде интервала с определенным шагом: F:=2,4..10 (первое и последнее число показывают границы интервала, разность между первым и вторым числами показывает шаг перебора). Шаблон графика вызывается из меню: Вставка – График – Х-У-участок. На горизонтальной оси на месте черного квадрата помещается переменная, ранее заданная в интервале с шагом (а). При записи функции в скобках должны быть указаны все переменные (но не константы), в том числе подстрочные индексы: b(a,i,j). На вертикальной оси помещается функция, у которой интервальная переменная задается в общем виде, а подстрочные индексы – конкретными номерами вариантов: b(a,0,2). После набора запятой (,) курсор перемещается строчкой ниже для записи другого варианта функции. После «клика» вне поля рисунка на графике появляются зависимости разных цветов.

При записи функции после имени в скобках указать все переменные, в том числе подстрочные индексы. Не забывать знак операции умножения.