20. Наивероятнейшее число «успехов» в серии n испытаний по схеме Бернулли.

Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов   (появлений события) имеет вид:

Так как  , то эти границы отличаются на 1. Поэтому  , являющееся целым числом, может принимать либо одно значение, когда   целое число ( ) , то есть когда  (а отсюда и  ) нецелое число, либо два значения, когда   целое число.

Пример. При автоматической наводке орудия вероятность попадания по быстро движущейся цели равна 0,9. Найти наивероятнейшее число попаданий при 50 выстрелах.

Решение. Здесь  . Поэтому имеем неравенства:

Следовательно,  .

21. Случайная величина как функция, ее область определения и область значений. Примеры.

Случайной величиной (СВ) Х() называется функция элементарного события  такая, что событие {: X()  x} принадлежит -алгебре F при любом действительном x. Область определения – пространство элементарных событий. Значения x функции Х() называются реализациями СВ Х(). Область значений – множество значений Х. Законом распределения случайной величины называется любое правило (таблица, функция), позволяющее находить вероятности всех возможных событий, связанных с СВ.

22. Классификация случайных величин по типу структуры множества их возможных значений.

СВ называется дискретной (СВДТ), если множество ее возможных значений конечно или счетно. Простейшей формой закона распределения дискретной СВ с конечным множеством значений является ряд распределения p_k = (по определению) P{X = x_k}, k=0,n, который задается аналитически или таблицей. В полученном ряду распределения сумма всех вероятностей равна единице.

СВ Х с непрерывной функцией распределения F_x(x) называется непрерывной. (СВНТ)

(Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно – это определение нестрогое).

23. Способы задания свдт.

Опр.: Закон распределения СВ – это всякое соотношение устанавливающее связь между возможными значениями СВ и соответствующими ими вероятностями. Говорят, что СВ распределена по данному закону или подчинена этому закону распределения.

ЗАКОН распределения СВДТ может быть задан в виде таблицы:

х1	х2	…	хn
p1	p2	…	pn

Х:

x1	x2	x3	...	xn	...
p1	p2	p3		pn

- ряд распределения СВДТ

где, х_1, х_2,…, х_n – возможные значения СВ, в порядке возрастания

p₁, p₂,..., p_n – соответствующие им вероятности.

Очевидно, что суммы вероятностей p_i=1

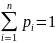
Т.к.события Х=х, х=1,…,х= х_n образуют полную группу событий.

Существует три способа задания: в виде таблицы, аналитически (в виде формулы) и графически: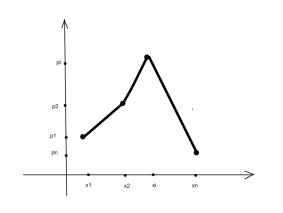

Ломаная, изображенная на этом рисунке, называется полигоном распределения вероятности.