17. Применение формулы Бернулли при решении двух основных задач в схеме Бернулли.

Пример. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.

Решение. Событие А – достали белый шар. Тогда вероятности ,  .  По формуле Бернулли требуемая вероятность равна  .

Пример. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.

Решение. Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А - «появление нестандартной детали», его вероятность  , тогда  . Отсюда по формуле Бернулли находим .

18. Применение формулы Пуассона при решении двух основных задач в схеме Бернулли.

Использование формулы Бернулли при больших n и m вызывает трудности из-за громоздких вычислений => возникает необходимость в отыскании вероятности 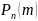обеспечивающих необходимую точность.

Теорема: если число испытаний неограниченно увеличивается n и вероятность р наступления соб.А в каждом испытании уменьшается р , но так что их произведение n*p остается величиной постоянной (λ=np=const), то вероятность

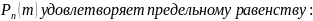
Доказательство: λ=np => p=λ/n подставляем это равенство в формулу:

= = =

Перейдем к пределу в обеих частях неравенства при n :

,

=>

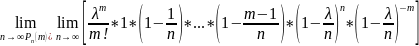
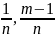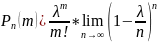
Формулу Пуассона применяют обычно когда n≥50, np≤10

Пример: Крымский завод отправил в Москву 1500 бутылок вина; вероятность того, что в пути бутылка может разбиться = 0,002. Найти вероятность того, что будет разбито в пути 4 бутылки.

Решение:

з-н Пуассона

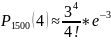
19. Применение формул Муавра-Лапласа при решении двух основных задач в схеме Бернулли.

В тех случаях, когда число испытаний n велико, а вероятность р близка к 0 (р≠0,р≠1) для вычисления вероятности используют локальную теорему Муавра-Лапласа.

Теорема: если вероятность р наступления соб.А в каждом испытании постоянна и отлична от 0 и 1, а число независимых испытаний достаточно велики, то вероятность Р_n(m) может быть вычислена по приблизительной формуле:

(х), где х=

Приблизительное равенство оказывается тем точнее, чем больше n (npq≥20)

Функция (х).

Выражение (х)= – формула Гаусса, её график называют кривой вероятности.

Функция (х) табулирована, но при пользовании таблицей следует учитывать свойства функции (х):

1 º. (-х)=, т.е. ф-ция четная

2º. _max(0)=0,3989

3º. при /х/≥4, (х)=0

Пример. Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 280 деталей отличного качества.

Решение. По условию  , откуда

По таблицам найдем  .

Искомая вероятность равна: 

Интегральная теорема Лапласа: если вероятность р наступления соб.А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число m наступления соб.А в n независимых испытаниях заключено в пределах от а до b включительно при достаточно большом числе n≈:

t₁)- t₂)

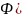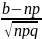t_{1= ,} t_{2= ,}

Ф(х)- интегральная схема Лапласа

Ф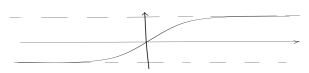 (х)= - интегральная формула Лапласа.

Значение ф-ции Ф(х) табулировано. Для применения таблицы необходимо знать свойства ф-ции:

1º. Ф(х)= -Ф(х), т.е нечетная

2º. При х≥5 Ф(х)=0,5; при х≥-5 Ф(х)=-0,5

Пример. В продукции некоторого производства брак составляет 15%. Изделия отправляются потребителям (без проверки) в коробках по 100 штук. Найти вероятности событий:

В – наудачу взятая коробка содержит 13 бракованных изделий;

С – число бракованных изделий в коробке не превосходит 20

Решение. Изготовление детали – это испытание, в котором может появиться событие А – изделие бракованное – с вероятностью  . Находим  . Можно применять формулы Лапласа:

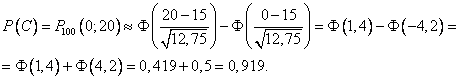
Приблизительно 9,5% всех коробок содержат 13 бракованных изделий и в 92% коробок число бракованных не превосходит 20.