14. Формула Байеса.

Из формулы полной вероятности следует:

Данная формула используется для переоценки вероятности гипотез при неизвестном результате.

15. Схема Бернулли: n однотипных независимых испытаний. Основные задачи в схеме Бернулли.

Опр.: несколько опытов называются независимыми, если их исходы представляют собой независимые в совокупности события; другими словами если опыт выполняется при данном комплексе условий многократно, причем наступление некоторого соб.А в каждом испытании не зависит от исхода других испытаний, то такие испытания называются независимыми.(Пример: подбрасывание монеты, стрельба по мишени без поправок на ошибку при повторном выстреле)

Опр.: последовательность n независимых испытаний в каждом из которых может про изойти некоторое событие А с вероятностью Р(А)=р, или соб.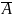 с вероятностью Р( )=1-q называется схемой Бернулли. (Пример: при подбрасывании монеты, соб А выпадение герба, соб. - выпадение орла.)

Примеры:

1. Имеется 5 студенческих групп по 25 человек, в каждой из которых по 5 отличников. Из каждой группы выбирается случайным образом по одному студенту. Найти вероятность того, что среди выбранных студентов будет 3 отличника.

Решение:

Вероятность выбрать отличника в одной группе равна p=1/5.Выбор отличника будем считать успехом. Тогда число успехов среди n=5 испытаний должно равняться m=3. Таким образом, по формуле Бернулли искомая вероятность равна 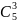(1/5)³(4/5)²= (32/625).

2. Вероятность появления успеха равна 3/5. Найти наивероятнейшее число наступлений успеха, если число испытаний равно 19, 20. Решение: при n =19 находим Таким образом, максимальная вероятность достигается для двух значений m₀, равных 11 и 12. Эта вероятность равна P₁₉(11)=P₁₉(12)=0,1797. При n=20 максимальная вероятность достигается только для одного значения m₀, т.к. 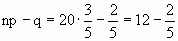не является целым числом. Наивероятнейшее число наступлений успеха m₀ равно 12. Вероятность его появления равна P₂₀(12)=0,1797. Совпадение чисел P₂₀(12) и P₁₉(12) вызвано лишь сочетанием значений n и p и не имеет общего характера.

16. Визуализация опыта, удовлетворяющего схеме Бернулли. Вывод формулы Бернулли.

Теорема: если производится n-независимых испытаний, в каждом из которых вероятность появления соб.А=р, а вероятность его не появления q=1-р, то вероятность того, что соб. А произойдет ровно m раз, вычисляется по формуле Бернулли:

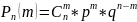
m=1,2,…,n

Доказательство: найдем вероятность того, что соб.А ровно m раз появится в первых m опытах и n-m раз не появится в остальных опытах Р(А*…*А*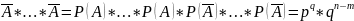

Найдем число слагаемых, для этого определим скольким числом способов можно расставить m штук А на n мест (характер выборки: неупорядоч., без повторений):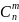 т.о.

m=1,2,…,n

совокупность вероятностей Р_n(0), Р_n(1), Р_n(2),…, Р_n(n), называется биномиальным законом распределения.

Следствие: если в серии из n независимых опытов в каждом из которых может произойти одно и только одно из k-событий А₁, А₂, А₃,…, А_k с вероятностями р₁, р₂, р₃,… р_k соответственно, то вероятность того, что соб.А_n появится вычисляется по формуле:

Р_n(m₁;m_2;…;m_k)=

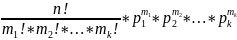
m₁+m₂₊…+m_k=n

Ломанная соединяющая точки с координатами (m; Р_n(m)), где m=1,2,…,n, называется многоугольником распределения вероятностей.