12. Зависимые и независимые события, их взаимность. Определение условной вероятности и следствие из него. Единственный способ установления зависимости событий.

Опр.: условной вероятностью соб.А называется вероятность соб.В при условии, что событие А произошло (пример: пусть соб.А - это извлечение из колоды в 32 карты туза; соб.В – вторая вынутая карта из колоды оказалось тузом. Если после 1-го раза карта возвращается в колоду, то вероятность вынуть туз не меняется и равна 4/32, если же 1-я карта в колоду не возвращается, то осуществление соб.А прибудет к тому, что в колоде остается 31 карта из которой 3 туза – условная вероятность

Теорема (умножения зависимых событий): вероятность произведения двух событий равна произведению вероятности одного события на условную вероятность другого, при условии, что 1-ое событие произошло:

Доказательство: Пусть n-число возможных исходов опыта; m_А-число исходов благоприятствующих соб.А; m_B-//-соб.В, m_АВ – число исходов опыта, при котором происходят оба события,. для вычисления условной вероятности , множеством возможных исходов нужно считать m_А(т.к. А произошло), а множеством благоприятных исходов, необходимо считать исходы, при которых произошли и А, и В.

=>

(Пример: для поражения цели необходимо попасть в неё дважды. Вероятность 1-го попадания 0,2, затем она не меняется при промахах, но после 1-го попадания увеличивается в 2 раза. Найти вероятность того что цель будет поражена первыми двумя выстрелами.

Решение: соб.А – попадания при первом выстреле

Соб.В - //- при 2-ом выстреле

,

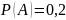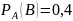
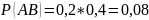
А и В совместные события)

Событие В называют независимым от события А, если появление соб.А не изменяет вероятности события В, т.е. если условная вероятность соб.В равна его безусловной вероятности:

подставив данное равенство в получим

, отсюда

,

т.е.условная вероятность соб.А в предположении, что наступило соб.В, равна его безусловной вероятности. Другими словами, соб.А не зависит от соб.В

Итак, если соб.В не зависит от соб.А, то и соб.А не зависит от соб.В; это значит, что свойство независимости событий взаимно.

Для независимых событий теорема умножения имеет вид

,

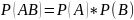Т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми.

На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий, поэтому событие «первое орудие поразило цель» и «второе орудие поразило цель» независимы.

13. Полная вероятность.

Опр.: полная группа несовместных событий - система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них. Сумма вероятностей всех событий в группе всегда равна 1.

Опр.: пусть событие А может произойти только совместно с одним из событий Н₁, Н₂,…,Н_n образующих полную группу несовместных событий, тогда соб. Н₁, Н₂,…,Н_n называются гипотезами.

Теорема: вероятность соб.А наступающего совместно с гипотезами Н₁, Н₂,…,Н_n равна:

- формула полной вероятности

где, Р(Н_i) – вероятность i-той гипотезы

Р_Нi(А) – вероятность соб.А при условии реализации гипотезы Н_i

Доказательство: соб.А можно считать суммой попарно несовместных событий АН_1, АН₂, …АН_n несовместные события, тогда из теорем сложения вероятностей:

Р(А)=Р(АН₁+…+ АН_n)=Р(АН₁)+…+Р(АН_n)=

=Р_Нi(А)* Р(Н₁)+…+ Р_Нn(А)* Р(Н_n)=