6. Операции над событиями. Алгебра событий.

Суммой (А+В) событий А и В называют событие состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий соответственно называют событие заключающееся в том, что произойдет хотя бы одно из этих событий.

2 стрелка делают по одному выстрелу по мишени. Если событие А- попадание 1-го стрелка, В-2-го, то сумма А+В – это хотя бы одно попадание при 2-х выстрелах.

Назовем всевозможные результаты данного опыта, его исходами и предположили, что множество этих исходов, при котором происходит соб.А, можно представить в виде некоторой области на плоскости. Тогда множество исходов, при которых произойдет соб.А+В является объединением множеств исходов благоприятных событиям А или В:

П роизведением А*В называется событие состоящее в том, что произошло и соб.А, и соб.В. Аналогично, произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события.(в условиях предыдущего примера, произведением будет попадание обоих стрелков).Диаграмма Эйлера-Венна

Операции над событиями обладают свойствами:

1.А+В=В+А, А*В=В*А

Переместительный з-н

2.(А+В)*С=А*С+В*С,

А*В+С=(А+С)*(В+С)

Распределительный

3. (А+В)+С=А+(В+С)

(А*В)*С=А*(В*С)

Сочетательный

4. А+А=А; А*А=А

5.А+u=A; A*u=A

u-достоверное событие

6.А+ =u; A* =v

u-достоверное соб.

v-невозможное соб.

Алгебра событий – алгебра подмножеств вероятностного пространства, элементами которого служат элементарные события. Она содержит пустое множество (невозможное событие) и замкнута относительно теоретико-множественных операций, производимых в конечном числе. Достаточно потребовать, чтобы алгебра событий была замкнута относительно двух операций, например, пересечения и дополнения (А*В и соответственно), из чего сразу последует её замкнутость относительно любых других теоретико-множественных операций. Алгебра событий, замкнутая относительно счётного числа теоретико-множественных операций, называется сигма-алгеброй событий.

7. Аксиоматическое определение вероятности.

Алгебра событий F, включающая в себя результаты сложения и умножения счетного числа своих элементов (т.е. замкнутая относительно этих операций), называется -алгеброй. Элементы -алгебры (т.е. подмножества пространства ) называются случайными событиями (или просто событиями). Вероятностью события А называется числовая функция Р(А), определенная на -алгебре и удовлетворяющая следующим четырем аксиомам теории вероятностей:

- Каждому событию А  F ставится в соответствие неотрицательное число Р(А), т. е. Р(А)  0 для любого А  F.

- Вероятность достоверного события равна единице, т. е. Р() = 1.

- Для любых несовместных событий А и В из F справедливо равенство Р(А + В) = Р(А) + Р(В).

- Для любой убывающей последовательности А₁  А₂  …  А_n  … событий из F, такой что A₁A₂A₃  ...  A_n  …=  , имеет место равенство

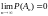
Аксиоматические свойства вероятности:

- Если Р(А) = 1, но А не равно , то говорят, что событие А в опыте G происходит почти наверное.

- Если Р(А) = 0, то говорят, что событие А почти никогда не происходит в опыте G.