37. Экспоненциальное распределение.

СВ Х имеет экспоненциальное (показательное) распределение с параметром  > 0, т. е. X ~ E(), если плотность вероятности имеет вид f(x) = exp(-x) при x > 0 и f(x) = 0 при x  0. Функция распределения СВ X ~ E() F(x) = 0 при x  0 и F(x) = 1 – exp[-x] при x > 0.

M[X] = 1/, D[X] = 1/², M[X²] = 2/².

Пример: Время X безотказной работы станка имеет экспоненциальное распределение. Вероятность того, что станок откажет за 5 часов работы равна 0,39347. Найти М[X], D[X], M[X²]. Решение: Найдем параметр распределения . Для этого решим уравнение:

1 – exp[-5] = 0,39347. exp[-5] = 0,60653. -5 = ln(0,60653) = -0,5.

 = 0,1. Теперь найдем необходимые моментные характеристики.

M[X] = 1/ = 10,

D[X] = 1/² = 100,

M[X²] = (M[X])² + D[X] = 200.

38. Нормальное распределение.

Пусть X ~ Bi(n,p). Тогда при n   Р((Х_n – np)/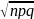  с)  Ф(c), где Ф(с) – функция Лапласа.

Ф(x) =

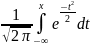
В справочниках часто встречается также функция Лапласа Ф₀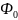(x).

(x) =

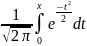
Ф(x) = ½ + Ф₀(x). Рассмотрим некоторые свойства функции Ф₀(x):

- Ф₀(-x) = -Ф₀(x).

- Ф₀(x) принимает значения от -½ до ½. Функция Ф(x) обладает всеми свойствами функции распределения, так как является функцией распределения стандартной нормальной случайной величины. Производная функции Ф((х-m)/) является функцией плотности вероятности нормальной СВ.

.

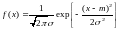Для стандартной нормальной СВ m = 0,  = 1.

Параметр m равен МО нормальной СВ, а параметр  есть квадратный корень из значения дисперсии нормальной СВ.

СВ X имеет нормальное (гауссовское) распределение с параметрами m и ² > 0, т.е. X ~ N(m, ²), если

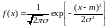
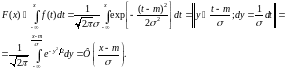
39. Правило «трех сигм» для нормального распределения вероятностей.

Нормально распределенная СВ с большей вероятностью принимает значения, близкие к своему МО, что описывает «закон трех сигм». Неравенство Чебышева: