29. Дисперсия свнт.

Т.к. дисперсия случайной величины есть математическое ожидание квадрата отклонения случайной величины от своего математического ожидания, то дисперсией непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называется определенный интеграл

   или

    .

При вычислении дисперсии СВНТ Х также можно пользоваться формулой

 Среднее квадратическое отклонение равно корню квадратному из дисперсии:

Св-ва D(x):

1)D(c)=0, где с - постоянная величина

2)D(k*x)= *D(x)

Док-во:D(k*x)=M = M = M

= D(x)

3)дисперсия D(x±y)=D(x)+D(Y)

4)D(x)=M(x²)-(M(x))²

Док-во:D(x)=M(x-M(x))²)=M(x²-2x*M(x)+M²(x))=M(x²)-2M(x)*M(M(x))+M(M²(x))=M(x²)-2M(x)*M(x)+M²(x)=M(x²)-M²(x)

30. Биномиальное распределение.

СВДТ Х с реализациями x_k = k, k=0,n, имеет биномиальное распределение с параметрами n и р  (0,1), если вероятность события Х = х_k определяется формулой Бернулли:

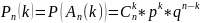
g(t) = ||бином Ньютона|| = (q+pe^it)ⁿ.

X ~ Bi(n,p). M(X) = np, D(X) = npq.

31. Бернуллиевское распределение.

Распределение Бернулли:

Распределение Бернулли есть частный случай биномиального распределения при n = 1.

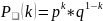
Y ~ Be(p). MY = p, DY = pq.

32. Геометрическое распределение.

Геометрическое распределение: это распределение дискретной случайной величины, равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».

Пусть Х1,…,Xn – конечная последовательность случайных величин с распределением Бернулли. Построим случайную величину Y = min{i | X_i=1} – 1 (Количество «неудач» до первого «успеха»). Распределение случайной величины Y называется геометрическим с вероятностью «успеха» p.

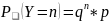
Y ~ Geom(p). М[Y]=р/(1-qе^t). D[Y]=q/р²

33. Гипергеометрическое распределение.

Гипергеометрическое распределение  моделирует количество удачных выборок без возвращения из конечной совокупности.

Пусть имеется конечная совокупность, состоящая из   элементов. Предположим, что   (defective) из них обладают нужным нам свойством. Оставшиеся   этим свойством не обладают. Случайным образом из общей совокупности выбирается группа из   элементов. Пусть   - случайная величина, равная количеству выбранных элементов, обладающих нужным свойством. Тогда:

,

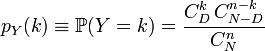М[Y]= ,

D[Y]=

34. Распределение Пуассона.

Теорема Пуассона: Между биномиальным распределением и распределением Пуассона имеется следующая связь: Пусть n  , p  0 и при этом np  a = const. Тогда:

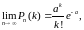Где

Доказывается эта теорема с использованием второго замечательного предела

(1-a/n)ⁿ  e^-a при n  .

СВДТ Х с реализациями xk = k, k = 0, 1, …, имеет распределение Пуассона с параметром a > 0, что символически записывается как Х ~ П(а), если .

M[X] = D[X] = a.

35. Равномерное дискретное распределение.

 СВДТ имеет равномерное распределение, если она принимает конечное число значений с равными вероятностями.

P(x=k) = ,

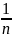M[X] =

D[X] =

36. Равномерное непрерывное распределение.

СВНТ Х распределена равномерно на отрезке [a,b] (Х ~ R(a,b)), если плотность вероятности имеет вид 1/(b-a) при х  [a,b] и 0 при х  [a,b]. Функция распределения имеет вид:

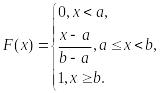
М[X] = (a+b)/2;

D[X] = (b-a)²/12;

M[X²] = (b²+ba+a²)/3.