Надання двовимірної величини за допомогою кореляційної таблиці

Х Y	10	15	20	25	30	35	40
40	2	2
50		5	12	8
60			11	25	15
70				4	10	1
80						3	2

Побудувати спряжені емпіричні лінії регресії і зробити припущення щодо форми кореляційного зв’язку та його щільності.

Р озв’язання. Доповнимо таблицю двома рядками і двома стовпцями (табл. 15.3). У першому допоміжному стовпчику (відповідно у першому допоміжному рядку) підрахуємо частоти, що відповідають сталому значенню однієї із випадкових величин. Відповідно, перший рядок таблиці і передостанній утворюють закон розподілу випадкової величини для вибіркової сукупності, перший і предостаній стовпці – закон розподілу випадкової величини . За значенням частот видно, що обидва закони можна вважати нормальними.

Кожний рядок таблиці вихідних даних у поєднанні з її першим рядком, що містить значення випадкової величини , є відображенням умовного закону розподілу за умов, що , а у додатковому стовпчику будемо вміщувати умовні середні випадкової величини . Наприклад, . Аналогічно обчислюємо умовні середні випадкової величини . Так, . Отже, отримуємо розширену таблицю (табл. 15.3).

Таблиця 15.3

Розширена кореляційна таблиця

Х Y	10	15	20	25	30	35	40
40	2	2						4	12,5
50		5	12	8				25	20,6
60			11	25	15			51	25,39
70				4	10	1		15	29
80						3	2	5	37
	2	7	23	37	25	4	2	100
	40	47,14	54,78	58,92	64	77,5	80

За даними табл. 15.3 побудуємо спряжені емпіричні лінії регресії та . Результати наведені на рис. 15.2.

З рис. 15.2 видно, що зв’язок між факторами та можна вважати статистично значущим, оскільки спряжені емпіричні лінії регресії розташовані близько одна до одної і кут нахилу між ними невеликий. Крім того, можна припустити, що цей зв’язок є лінійним і прямо пропорційним, оскільки із зростанням фактора значення фактора збільшується, а також із зростанням фактора значення фактора збільшується.

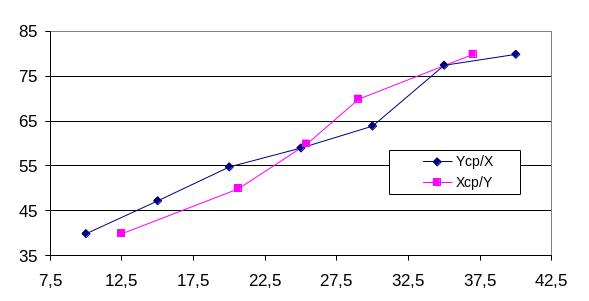
Рис. 15.2. Емпіричні лінії регресії та

О тже, оскільки зв’язок між факторами, що досліджуються, є статистично значущим, доцільно подовжувати дослідження.