2.3.3. Метод Гуро

Метод Гуро - способ закрашивания граней трехмерных объектов, который использует интерполяцию интенсивностей отражения света в вершинах граней.

Этот метод предназначен для создания иллюзии гладкой криволинейной поверхности, описанной в виде многогранников или полигональной сетки с плоскими гранями. Если каждая плоская грань имеет один постоянный цвет, определенный с учетом отражения, то различные цвета соседних граней очень заметны, и поверхность выглядит именно как многогранник. Казалось бы, этот дефект можнo замаскировать за счет увеличения количества граней при аппроксимации поверхности. Но зрение человека имеет способность подчеркивать перепады яркости на границах смежных граней  такой эффект называется эффектом полос Маха. Поэтому для создания иллюзии гладкости нужно намного увеличить количество граней, что приводит к существенному замедлению визуализации  чем больше граней, тем меньше скорость рисования объектов.

Метод Гуро основывается на идее закрашивания каждой плоской грани не одним цветом, а плавно изменяющимися оттенками, вычисляемыми путем интерполяции цветов примыкающих граней. Закрашивание граней по методу Гуро осуществляется в четыре этапа:

• вычисляются нормали к каждой грани;

• определяются нормали в вершинах;

• нормаль в вершине определяется усреднением нормалей примыкающих граней (рис. 2.2);

• на основе нормалей в вершинах вычисляются значения интенсивностей в вершинах согласно выбранной модели отражения.

Закрашиваются полигоны граней цветом, соответствующим линейной

интерполяции значений интенсивности в вершинах

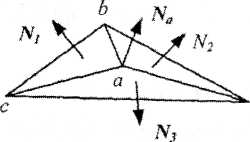
Рис. 2.2. Нормаль в вершине

Вектор нормали в вершине (а) равен: N_a=(N₁+N₂+N₃)/3 .

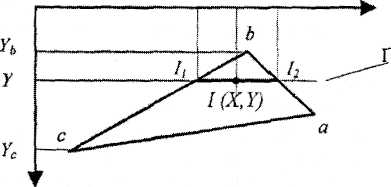
Определение интерполированных значений интенсивности отраженного света в каждой точке грани (и, следовательно, цвет каждого пиксела) удобно выполнять во время цикла заполнения полигона. Рассмотрим заполнение контура грани горизонталями в экранных координатах (рис. 2.3).

Х₁ Х Х₂

Рис. 2.3. Заполнение контура грани

Интерполированная интенсивность I в точке (X,Y) определяется исходя из пропорции (I – I₁)/(Х  Х₁)=(I₂ – I₁)/(Х₂ X₁).

Отсюда I = I₁ + (I₂ – I₁) (X  Х₁)/(Х₂ X₁).

Значения интенсивностей I₁ и I₂ на концах горизонтального отрезка представляют собой интерполяцию интенсивности в вершинах:

(I₁ I_b) /(YY_b) = (I_c I_b) /(Y_c Y_b)

(I₂ I_b) /(YY_b) = (I_a I_b) /(Y_a Y_b)

Или

I₁ =I_b + (I_c I_b) (YY_b) /(Y_c Y_b)

I₂ =I_b + (I_a I_b) (YY_b) /(Y_a Y_b)

2.3.4. Метод Фонга

Метод Фонга - способ закрашивания граней трехмерных объектов, который основывается на интерполяции векторов нормалей в вершинах.

Аналогичен методу Гуро, но при использовании метода Фонга для определения цвета в каждой точке интерполируются не интенсивности отраженного света, а векторы нормалей.

• определяются нормали к граням;

• по нормалям к граням определяются нормали в вершинах. В каждой точке закрашиваемой грани определяется интерполированный вектор нормали;

• по направлению векторов нормали определяется цвет точек грани в соответствии с выбранной моделью отражения света.

Рассмотрим, как можно получить вектор нормали в каждой точке грани. Для интерполяции будем оперировать векторами N'_a, N'_b, и N'_c, исходящими из центра координат плоскости проецирования и параллельными соответствующим нормалям N_a, N_b и N_c в вершинах a, b и с (рис. 2.4)

Рис. 2.4. Интерполяция векторов нормалей

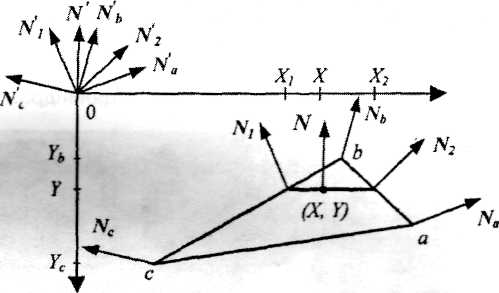
Вектор N' параллелен вектору N для нормали в точке (X, Y), поэтому его можно использовать для расчета отражения света так же, как и вектор нормали N.

Метод Фонга сложнее, чем метод Гуро. Для каждой точки (пиксела) поверхности необходимо выполнять намного больше вычислительных операций. Тем не менее, он дает значительно лучшие результаты, в особенности при имитации зеркальных поверхностей.

Общие черты и отличия методов Гуро и Фонга можно показать на примере цилиндрической поверхности, аппроксимированной многогранником (рис. 2.5). Пусть источник света находится позади нас. Проанализируем закрашивания боковых граней цилиндра.

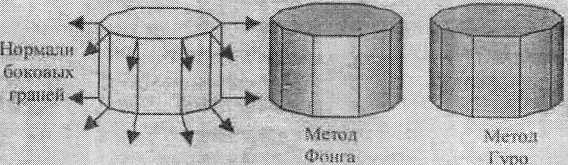
Рис. 2.5. Отличия закрашивания Фонга и Гуро

На рис. 2.5 на закрашенной поверхности показаны черным цветом ребра граней — это сделано для иллюстрации особенностей закрашивания, на самом деле после закрашивания никакого черного каркаса не будет, и поверхность выглядит гладкой.

Основные отличия можно заметить для закрашивания передней грани. Она перпендикулярна направлению лучей света. Поэтому нормали в вершинах этой грани располагаются симметрично — они образовывают попарно равные по абсолютной величине углы с лучами света. Для метода Гуро это обуславливает одинаковые интенсивности в вершинах передней грани. А раз интенсивности одинаковые, то и для любой точки внутри этой грани интенсивность одинакова (для линейной интерполяции). Это обуславливает единый цвет закрашивания. Все точки передней грани имеют одинаковый цвет, что, очевидно, неправильно.

Метод Фонга дает правильное закрашивание. По методу Фонга центр передней грани будет светлее, чем края.