РОСЖЕЛДОР

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Ростовский государственный университет

путей сообщения

Е.В. Голубенко

Компьютерная геометрия и графика

Часть 2

Алгоритмы и методы 3Dграфики

Конспект лекций

Ростов-на-Дону

2008

1. Модели описания поверхностей

1.1 Виды геометрических моделей, их свойства

В компьютерной графике (КГ) объект можно представить в виде каркасной (проволочной), поверхностной (полигональной) и твердотельной (объемной) моделей (рис. 1.1).

Каркасная модель - изображение объекта, которое содержит только прямые линии.

Поверхностная (полигональная) модель - изображение объекта, которое содержит точки, линии и поверхности.

Геометрический примитив - точка, линия или многоугольник.

Конструктивными элементами проволочной модели являются ребро и точка. Эта модель проста, но с ее помощью можно представить в пространстве только ограниченный класс деталей, в которых аппроксимирующие поверхности преимущественно являются плоскостями. На основе пространственной проволочной модели можно получать, например, проекции объекта на чертеже. Однако с помощью проволочных моделей не всегда возможно получить правильные изображения, а также автоматически анализировать процессы удаления невидимых линий и получения различных сечений.

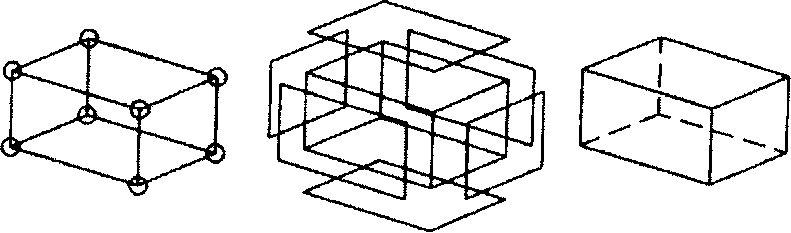
а) б) в)

Рис.1.1. Виды моделей геометрического объекта: а - каркасная (проволочная);

б - полигональная (поверхностная); в - объемная (твердотельная)

При создании полигональной модели предполагается, что объекты ограничены поверхностями, которые отделяют их от окружающей среды. Такая оболочка тела графически изображается поверхностями.

С помощью полигональной модели можно описать любую поверхность объекта, содержащую наряду с плоскими многоугольниками поверхности второго порядка и аналитически прописываемые поверхности. Это реализуется путем аппроксимации поверхностей многогранником, каждая грань которого является простейшим плоским многоугольником (треугольник, четырехугольник, рис. 1.2). Чем больше число граней, тем меньше отклонение от действительной формы объекта.

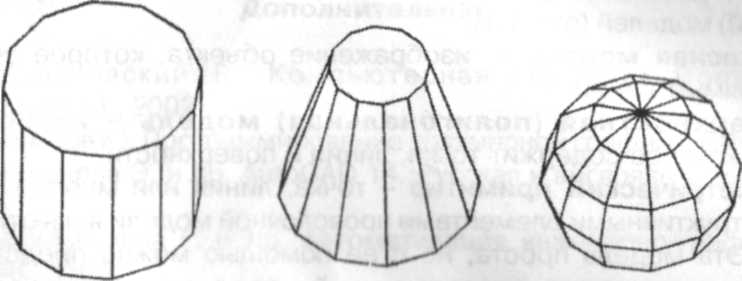
Рис.1.2 Аппроксимация плоскостями

Если объект представлен полигональной моделью, то всегда можно определить область между контурными элементами этого объекта. Эту область, включая ее границы, рассматривают как единое целое, что значительно упрощает описание объекта, позволяет производить автоматическую штриховку таких областей, а также копирование и преобразование модели объекта. Кроме того, над полигональными моделями объектов можно выполнять логические операции объединения, вычитания, пересечения.

Поверхностные модели по способам описания поверхностей подразделяются на:

• аналитические;

• векторные;

• воксельные;

• равномерная сетка;

• неравномерная сетка;

• изолинии.

В основу описания объекта объемной моделью положен принцип формирования сложной геометрической структуры из элементарных объемов (базисных тел) с использованием логических операций объединения, вычитания и пересечения.