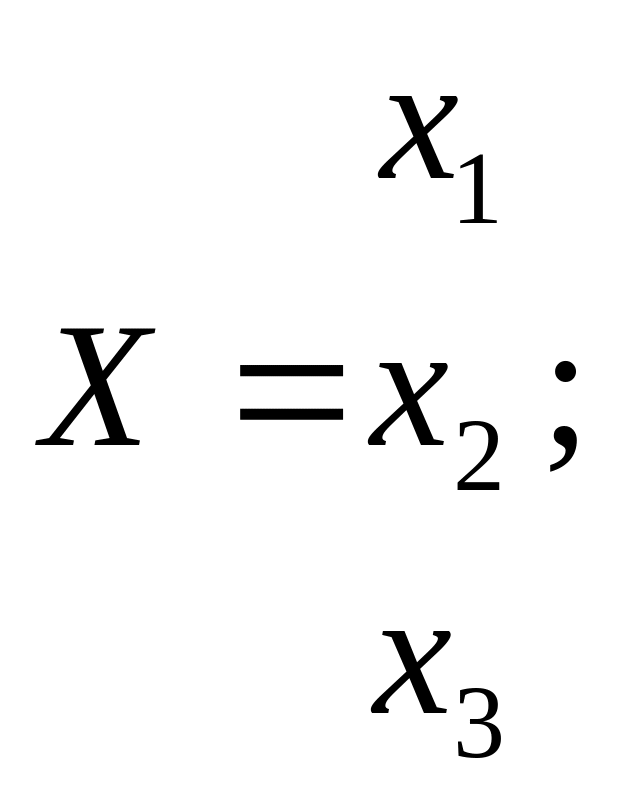1. Побудова моделі без вивчення структури об'єкта (об'єкт-"чорна скринька").

У цьому випадку при моделюванні не беруться до уваги внутрішні параметри. Математична модель описує зв'язок між зовнішніми параметрами:

Якщо дія зовнішнього середовища на технічний об'єкт, наприклад, описується вектором X, що складається із трьох факторів х1, х2, х3, а результат цієї дії визначиться вектором-показником Y(y1,y2,y3), то модель матиме такий вигляд:

Розв'язання цієї системи рівнянь дає змогу перейти до складових простих моделей, що описують технічний об'єкт:

Для компактності застосовується форма запису у вигляді матриці

,

де матричні елементи залежності мають такий вигляд:

Така модель не описує внутрішню структуру технічного об'єкта, тому вона використовується для опису елементів структури.

2. Моделі, побудовані з декількох елементів

Коли в об'єкті дослідження вдається виділити окремі елементи та простежити їх зв'язки між собою, процес моделювання стає простішим. Однак у випадках, коли прості явища та їх моделі, що входять до складу досліджуваного об'єкта, відомі, але характер їх зв'язків невідомий, то модель будується добиранням можливих зв'язків між простими моделями, перевіркою кожного варіанта моделі й вибором точнішої.

Наприклад, для побудови моделей, що описують поведінку при деформуванні реальних матеріалів, використовуються лише дві елементарні моделі: модель Гука, що описує поведінку абсолютно пружного тіла, та модель Ньютона, що описує поведінку рідини. Однак різне поєднання цих моделей (паралельне, послідовне, послідовно-паралельне тощо) дає змогу побудувати досить точні моделі, що описують поведінку холодних і нагрітих металів, пластмас, бетонних сумішей, асфальтів тощо. Розглянемо ці елементарні моделі.

Пружне тіло Гука (рис. 7, а) — це тверде тіло, що має здатність відновлювати свої форму та об'єм після припинення дії зовнішніх сил.

Залежність між напруженнями σ і деформаціями ε у пружному тілі є прямо пропорційною і описується законом Гука

,

де E — модуль пружності матеріалу.

Графік цієї залежності являє собою пряму, що проходить через початок системи координат. Тангенс кута нахилу цієї прямої до осі е відповідає модулю пружності матеріалу Е. Ця залежність справджується тільки для деформацій, що відбуваються в межах пружності матеріалу, тому вона є моделлю, що описує пружні властивості матеріалів. Схематично модель Гука позначимо у вигляді пружини (рис. 7, а).

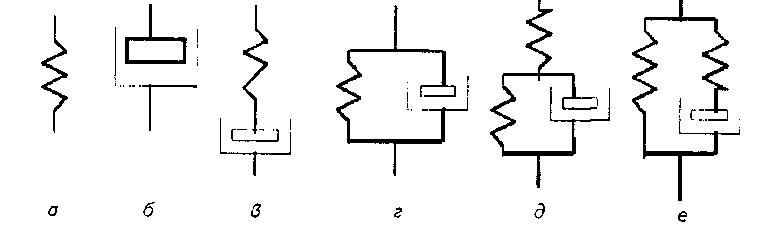
Рис.7. Конструювання складних моделей для опису механічних властивостей матеріалів.

У реальних твердих тілах, окрім пружних, відбуваються і пластичні деформації, під дією яких форма твердого тіла змінюється. Відбувається плин матеріалу. Інша властивість деформівних тіл, а саме їх в'язкість, описується моделлю Ньютона. Залежність напружень σ від швидкості деформації для ньютонівської моделі визначиться таким чином:

,

де η — коефіцієнт динамічної, або ньютонівської, в'язкості.

Якщо напруження σ виражене в , а ε — відносна деформація є безрозмірною величиною, то в'язкість матиме розмірність . Графіки залежності напружень від швидкості деформування називають кривими плину.

Розглянуті моделі Гука та Ньютона — прості моделі, які легко піддаються математичним перетворенням. Різні структурні варіанти поєднання простих моделей Гука і Ньютона, що описують пружність і плинність матеріалів, дають змогу отримувати моделі матеріалів зі складною поведінкою (пластмаси, смоли, пасти тощо). Але для цього необхідно знати характер зв'язку між простими моделями, щоб отримана складна модель точно описала поведінку реального матеріалу. Вибір структури складної моделі здійснюється шляхом добору — будується модель, де елементарні моделі Гука і Ньютона з'єднуються послідовно або паралельно, потім експериментально досліджується поведінка матеріалу і порівнюється із результатами прогнозування за моделлю. Якщо необхідно, модель ускладнюється.

При послідовному зв'язку простих моделей (рис.7, в) повна деформація є складатиметься із деформацій пружного ε₁ і в'язкого ε₂, елементів, а напруження в обох елементах будуть однакові й рівні σ, тобто:

При паралельному зв'язку простих моделей (рис.7, г) повне напруження σ складатиметься із напружень у пружному σ₁ і напружень у в'язкому σ₂ елементах, а деформації ε в обох елементах будуть однакові, тобто

Використовуючи послідовне або паралельне об'єднання простих моделей, можна побудувати моделі, що опишуть деформування різних матеріалів (рис.7). Розглянемо типові двоелементні моделі.

Модель Максвелла (рис. 7, в), в якій моделі пружного і в'язкого елементів з'єднані між собою послідовно, описує взаємний зв'язок між напруженнями та деформаціями в матеріалі в такому вигляді:

.

Ця модель отримана за правилами послідовного з'єднання елементів. Модель Кельвіна (рис. 7, г), в якій моделі пружного і в'язкого елементів з'єднані між собою паралельно, має такий вигляд:

.

Модель Кельвіна широко застосовується для опису поведінки полімерних матеріалів.

Для опису поведінки високополімерних матеріалів використовуються трьохелементні моделі, створені шляхом приєднання другого пружного елемента E₂ до двоелементних моделей Кельвіна та Максвелла (рис. 7, д, е). Розглядаючи двоелементні моделі як елементарні, що з'єднані з елементом E₂, отримаємо за правилами послідовного чи паралельного з'єднання описи трьохелементних моделей:

;

.

У розглянутих прикладах побудова складної моделі здійснюється паралельним або послідовним об'єднанням простих моделей. Однак більшість реальних об'єктів має складнішу структуру, тому побудувати їх моделі важко. В таких випадках для зв'язків між елементами об'єкта, що можуть бути описані простими моделями, часто використовуються методи теорії графів.