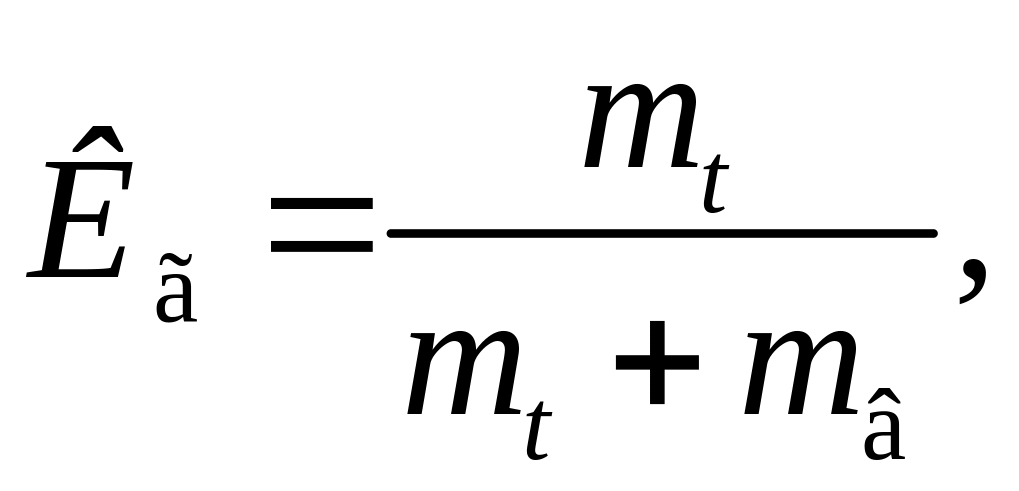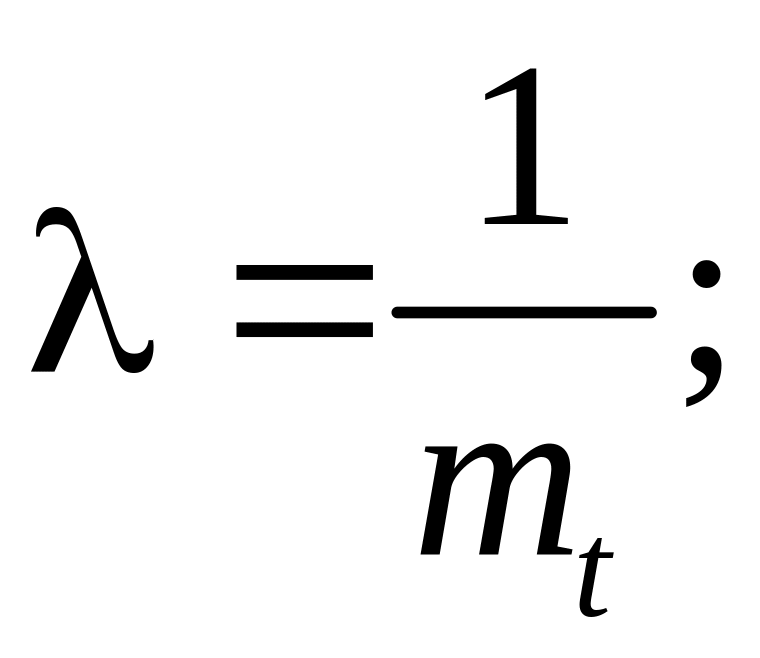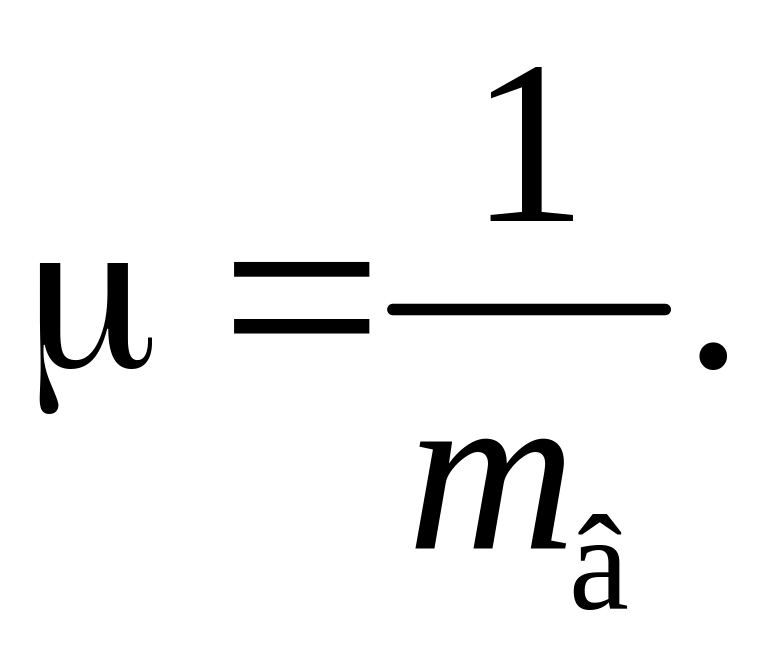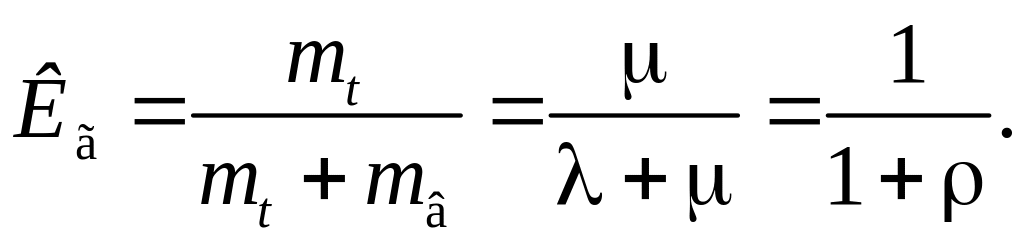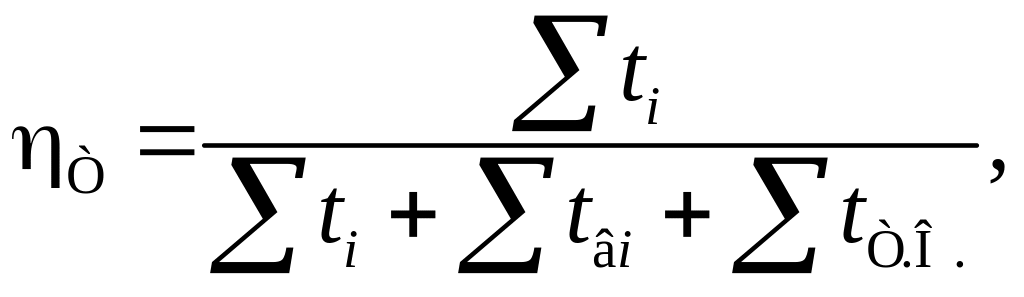2.4.2. Показники безвідмовності технологічної системи

Показники безвідмовності відновлюваних об'єктів, до яких нале­жать технологічні системи, ґрунтуються на понятті наробки між відмо­вами. Наробка між відмовами t₁, t₂, ... (рис. 2.6) визначається як наробка об'єкта від закінчення відновлення його працездатного стану після відмови до виникнення наступної відмови.

Ймовірність безвідмовної роботи P(t_i) - це ймовірність того, що упродовж заданої тривалості функціонування t_i відмова об'єкта не ви­никне. Вона пов'язана з імовірністю виникнення відмови F(t_i) наступ­ним чином:

.

Ймовірність відмови F(t_i) визначається як ймовірність того, що об'єкт відмовить хоча б один раз упродовж заданого часу функціонування t_i, якщо він був працездатний у початковий момент часу.

Середня наробка на відмову m_t — це відношення наробки віднов­люваного об'єкта до математичного сподівання числа його відмов п у процесі цієї наробки. Середня наробка на відмову визначає наробку відновлюваного об'єкта, що припадає в середньому на одну відмову при певній тривалості експлуатації. Вона визначається як

.

Параметр потоку відмов — це відношення середнього числа відмов відновлюваного об'єкта за довільно малу його наробку до зна­чення цієї наробки.

Оскільки для відновлюваного об'єкта моменти відмов на осі часу (без урахування часу відновлення) утворюють потік відмов, то характе­ристикою цього потоку буде провідна функція , яка визначає мате­матичне сподівання числа відмов за час

де — число відмов за час .

Тоді параметр потоку відмов характеризуватиме середню кількість відмов у малому інтервалі часу

Залежно від властивостей потоку відмов вираз для параметра може бути спрощений. Це буде у випадку, якщо потік відмов матиме властивості стаціонарності, ординарності та відсутності післядії.

Ординарним називається потік подій, для якого ймовірність потрап­ляння на малий інтервал часу двох або більше подій є величиною, якою нехтуємо стосовно ймовірності потрапляння однієї події.

Потік без післядії передбачає перебіг подій незалежно одна від од­ної.

Стаціонарним називається потік, у якому ймовірність надходження того чи іншого числа подій протягом певного інтервалу часу залежить від тривалості цього інтервалу і не залежить від його положення на осі часу.

Для стаціонарного потоку подій , а провідна функція

Потік, який має властивості ординарності, відсутності післядії та стаціонарності, називають найпростішим, або однорідним пуасонівським. Якщо розподіл часу між відмовами в такому потоці є експоненцій-ним, то параметр потоку відмов it' відповідатиме інтенсивності відмов , тобто

Інтенсивність відмов — це умовна кількість ймовірності відмови невідновлюваного об'єкта, що визначається для даного моменту часу за умови, що до цього моменту відмова не виникла.

2.4.3. Комплексні показники надійності відновлюваних об'єктів

Вони визначають деякі характеристики надійності. Для технологіч­них систем найбільш широко використовуються комплексні показники надійності, які характеризують їх безвідмовність та ремонтопридатність.

Розглянемо показники ремонтопридатності: ймовірність відновлен­ня працездатного стану за час та середній час відновлення , що визначається як (див. рис. 2.6):

До комплексних показників надійності, які характеризують без­відмовність та ремонтопридатність технологічних систем, належить, передусім, коефіцієнт готовності , який визначає ймовірність того, що технологічна система буде в працездатному стані у довільний мо­мент часу, окрім запланованих періодів, під час яких її використання за призначенням не передбачено,

де — середня наробка на відмову та середній час відновлення технологічної системи.

Оскільки коефіцієнт готовності є характеристикою усталеної робо­ти технологічної системи, то його значення не залежить від законів розподілу випадкових величин та . Тоді інтенсивності потоку відмов та потоку відновлень можуть бути визначені як

Якщо позначити завантаженість технологічної системи відновлювальними роботами через 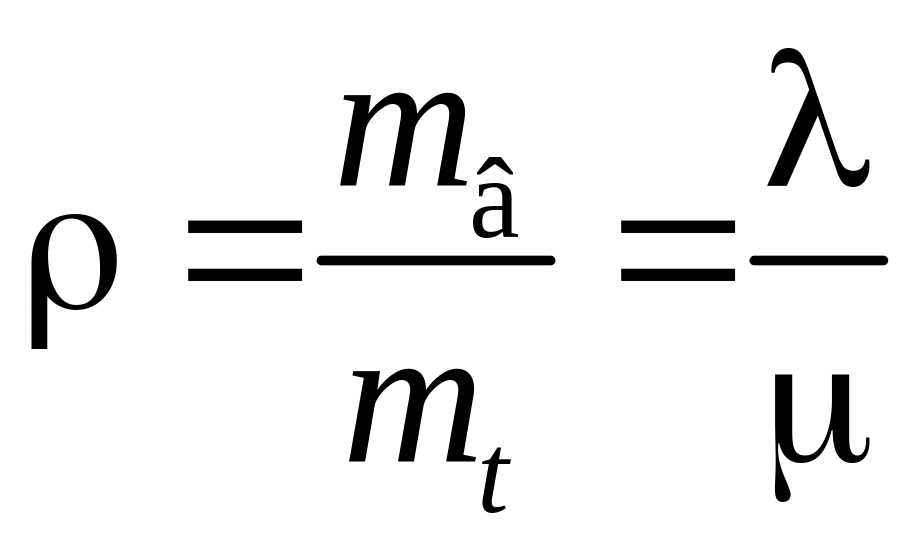, то вираз для визначення коефіцієнта готовності набуде вигляду

Величина, обернена до коефіцієнта готовності, називається коефі­цієнтом простоювання , який визначається як

Якщо врахувати, що в реальних умовах функціонування технологіч­них систем , то

При визначенні коефіцієнта готовності не беруться до уваги періо­ди часу, коли об'єкт зайнятий плановим технічним обслуговуванням. Ці періоди часу враховуються за допомогою іншого показника функці­онування технологічної системи — коефіцієнта технічного викорис­тання , який визначається відношенням математичного сподівання інтервалів часу, коли технологічна система була у працездатному стані за деякий період експлуатації, до суми математичних сподівань інтер­валів часу перебування технологічної системи в працездатному стані , простоювань, зумовлених технічним обслуговуванням та ремонтом за цей же період експлуатації, тобто

де — сумарний час технічного обслуговування за заданий період експлуатації.
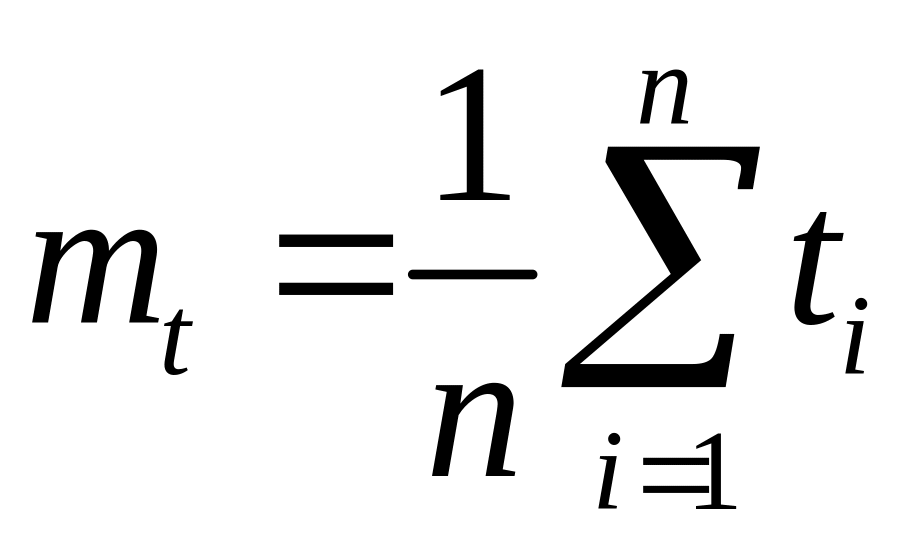