7. Опис оптимальних демодуляторів

Демодулятора надходить сума переданого модульованого сигналу s(t) і завади n(t):

z(t) = s(t) + n(t)

Демодулятор повинен відновити цифровий сигнал. Критерієм оптимальності є мінімум ймовірності помилки двійкового символу(бітд) цифрового сигналу.

Сигнал цифрової модуляції s(t) – це послідовність радіоімпульсів, що відображають цифровий сигнал і проходять через тактовий інтервал Т:

s(t)=±sl^k\t-kT)

деs'0-кТ)- і-ій радіоімпульс, що передається на к-му тактовому інтервалі

Радіоімпульси можуть відрізнятися амплітудами, фазами або частотами. Існують різні види цифрової модуляції АМ-2, ФМ-2, ЧМ-2, КАМ-2, АФМ-2. При цьому радіоімпульс використовується для передавання 0, а радіоімпульс s_i(t) - для передавання 1.

Таблиця. Опис елементарних сигналів

Метод модуляції
АМ-2	ЧМ-2	ФМ-2
0		=-

У даній таблиці використані наступні позначення:

а-коефіцієнт, що визначає енергію елементарного сигналу( 1-біта);

А(t) - функція, що описує форму елементарного сигналу;

f₀ - частота несійного коливання;

∆f – відхилення(девіація) частоти при ЧМ-2.

Під час демодуляції послідовності елементарних сигналів необхідно виконати дискретизацію з інтервалом Т в моменти часуt₀+kT,k = ...-1,0,1,2... Правильний вибір цих моментів забезпечує система тактової синхронізації(ТС).

На основі оцінки вирішуючою схемою виноситься рішення про переданий сигнал. Правило винесення рішення формулюється на основі сигналу, що демодулюється. Рішення виноситься шляхом порівняння оцінкиа з пороговим значенням

за правилом:a , то передавався сигналs,(t), а якщо a то

передавався сигналs₀(t). При АМ-2 а,=а, =0, = 0,5а,тобто порогове значення дорівнює половині відлікового значення з виходу УФ при надходженні на вхід демодулятора без завади.

Схема оптимального когерентного демодулятора BФМ-2

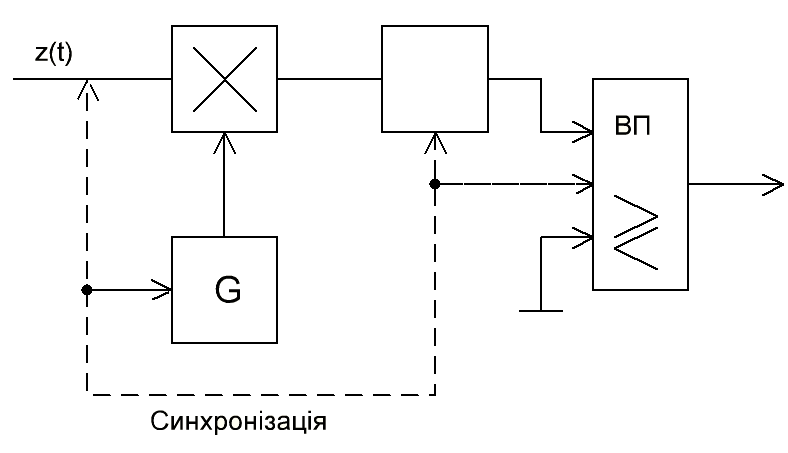
Рис. . Схема оптимального приймання сигналів із ЧМ-2

Доведено, що ця схема в еквівалентному вигляді може бути представлена на Рис 4, яка має в своєму складі амплітудні детектори. Тому схема приймання сигналів із ВФМ-2 за методом порівняння фаз часто у літературі називають схемою не когерентного приймання сигналів із ВФМ-2. Якщо різниця фаз двох сусідніх сигналів дорівнює нулю, то значення відліку сигналу у верхній гільці обробки дорівнює 2Е, а в нижній – 0. Якщо різниця фаз сусідніх сигналів ∆φ= то навпаки, у верхній гільці – 0, а у нижній – 2Е

З порівняння розглянутої схеми зі схемою некогерентного приймання ЧМ сигналів видно, що схеми відрізняються величиною значення відліку на вході АД. Тому формула для ймовірності помилки має такий вигляд:

8.Обчислення потенційної завадостійкості

Під потенційною завадостійкістю приймання дискретних сигналів розуміють мінімально можливу ймовірність помилки, якщо сигнали приймаються оптимальним приймачем.

Таблиця 7.1. Ймовірність помилки Р_пом при оптимальному прийманні дискретних сигналів

Тип сигналу	Когерентне приймання	Некогерентне приймання
ЧМ-2	0.5*Q(h)	-

Труднощі застосування формул , наведених у таблиці 7.1. полягають у необхідності мати таблицю інтеграла ймовірності . Тому ймовірність помилки при когерентному прийманні сигналів АМ-2, ЧМ-2, ФМ-2 можна визначати для технічних розрахунків за формулою:

, де:

відношення енергії сигналу до спектральної густини завади

Енергія сигналу вимірюється у В², а спектральна густина сигналу в В²/Гц

h²=