13.14. График зависимости между доходом (Х) и спросом на блага (Y) (например, на товары первой необходимости либо товары относительной роскоши), задаваемой моделью вида (так называемая функция Торнквиста, – минимально необходимый уровень дохода), имеет вид:

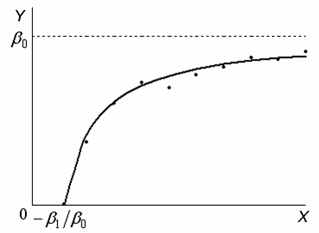
Тогда …

1) β₀ < 0 2) β₀ > 0 3) β₁ < 0 4) β₁ > 0

= = = = = = =

13. 15Для производственной функции Кобба-Дугласа ,

если b+c>1, то …

1) имеется возрастающая отдача от масштабов производства

2) имеется убывающая отдача от масштабов производства

3) имеется постоянная отдача от масштабов производства

13. 16Для производственной функции Кобба-Дугласа ,

если b+c<1, то …

1) имеется возрастающая отдача от масштабов производства

2) имеется убывающая отдача от масштабов производства

3) имеется постоянная отдача от масштабов производства

13. Для производственной функции Кобба-Дугласа ,

если b+c=1, то …

1) имеется возрастающая отдача от масштабов производства

2) имеется убывающая отдача от масштабов производства

3) имеется постоянная отдача от масштабов производства

13. 17При анализе эластичности спроса по цене целесообразно использовать следующую модель:

1) линейную;

2) полиномиальную;

3) логарифмическую;

4) степенную;

5) эксцоненциальную.

13.18 Модель вида , носит название:

1) полиномиальная

2) гиперболическая (обратная);

3) обращенная полиномиальная функция;

4) логлинейная;

5) обобщенная логарифмическая;

6) полулогарифмическая;

7) степенная;

8) экспоненциальная.

13. 19Модель вида носит название:

1) полиномиальная;

2) гиперболическая (обратная);

3) обращенная полиномиальная функция;

4) логлинейная;

5) обобщенная логарифмическая;

6) полулогарифмическая;

7) степенная.

13. 20Модель вида , носит название:

1) полиномиальная;

2) гиперболическая (обратная);

3) обращенная полиномиальная функция;

4) логлинейная;

5) обобщенная логарифмическая;

6) полулогарифмическая;

7) степенная.

13. 21Модель вида носят название:

1) полиномиальная;

2) гиперболическая (обратная); экспоненциальная;

3) степенная;

4) функция Гомперца;

5) логистическая;

6) показательная

13. 22Модель вида носит название:

1) полиномиальная;

2) гиперболическая (обратная);

3) экспоненциальная;

4) степенная;

5) функция Гомперца;

6) логистическая; показательная.

13. 23Модель вида носит название:

1) полиномиальная;

2) гиперболическая (обратная);

3) обращенная экспоненциальная;

4) степенная;

5) функция Гомперца;

6) логистическая;

7) показательная.

14.1. Для степенной регрессионной модели возможен

аддитивный способ включения случайного возмущения .

Для получения качественных оценок параметров этой модели …

1) возможно применение метода наименьших квадратов

2) требуется подобрать соответствующую подстановку

3) метод наименьших квадратов неприменим

4) необходимо выполнить логарифмическое преобразование

14.2. Уравнение вида является …

1) нелинейным только по параметрам, но линейным по переменным

2) нелинейным только по переменным, но линейным по параметрам

3) линейным как по переменным, так и по параметрам

4) нелинейным как по переменным, так и по параметрам ?

14.3. Нелинейным является уравнение регрессии нелинейное относительно входящих в него …

+1) факторов 2) результатов 3) параметров 4) случайных величин

14.4. Модель относится к классу ________ эконометрических моделей нелинейной регрессии

1) показательных

2) степенных

3) логарифмических

4) линейных

Такого ответа в вариантах нет, правильный ответ полиномиальных.

14.5 Установите соответствие между названием модели и видом уравнения:

1. линейная

2. полиномиальная

3. показательная

4. полулогарифмическая

1-А.

4- B.

2- C.

3- D.