Часть 2. Электродинамика поля зарядов и токов в вакууме
Лекция 3
10. Закон Кулона. Напряженность электрического поля. Теорема Гаусса
Закон Кулона
гласит, что два неподвижных заряженных
тела малых, по сравнению с расстоянием
между ними, размеров (два точечных
заряда) расположенные в вакууме
отталкиваются, если заряды их одноименные,
и притягиваются, если они разноименные,
причем сила их взаимодействия
(сила
действует на второй заряд со стороны
первого,
- наоборот)
пропорциональна величинам зарядов
и
,
обратно пропорциональна квадрату
расстояния между ними и направлена
вдоль линии, соединяющей заряды (рис.
2.1)
Для модулей:
(2.1)
Рис. 2.1. Иллюстрация закона Кулона
Здесь
‑ расстояние между первым и вторым
зарядом,
‑ единичный вектор, направленный от
первого ко второму заряду,
‑ коэффициент пропорциональности,
зависящий от выбора системы единиц.
Этот закон был установлен Кулоном в 1785 – 1789 гг.
Если взаимодействие происходит не в вакууме, а в воздухе, то, как показывает опыт, сила взаимодействия такая же (почти), как и в вакууме.
В системе единиц
СИ единица заряда называется кулон
(Кл). Из определения единицы силы тока
1А можно получить, что зарядом 1 Кл
называется такая величина заряда, что,
если поместить на расстоянии 1 м два
одинаковых заряда по 1 Кл каждый, то
они будут взаимодействовать с силой
.
Тогда из (2.1) легко находим
.
(2.2)
Здесь Ф – фарада (единица измерения емкости).
Вместо коэффициента
k
принято вводить коэффициент
.
Эти коэффициенты связаны соотношением
.
(2.3)
Тогда окончательно закон Кулона может быть записан в виде:
,
(2.4)
где, как легко найти из (2.2) и (2.3),
Для модулей
. (2.5)
Если взаимодействуют три или более точечных заряда, то при нахождении силы, действующей на какой-либо заряд, будем пользоваться принципом наложения (суперпозиции). Это опытный факт. Он состоит из двух положений:
– сила взаимодействия двух зарядов не зависит от того, подвергаются ли эти заряды воздействию других зарядов или нет;
– равнодействующая электрических сил равна векторной сумме этих сил.
Если в точках некоторого пространства обнаруживаются силы, действующие на неподвижный заряд, помещенный в эти точки, то будем говорить, что в этом пространстве существует электрическое поле. Заряд (неподвижный или движущийся) возбуждает в окружающем пространстве электрическое поле. Пока мы остаемся в пределах электростатики, понятие поля может рассматриваться как понятие чисто условное, введенное лишь для удобства описания электрических явлений. Однако, перейдя к учению о переменном электромагнитном поле, в частности, к учению об электромагнитных волнах, мы убедимся, что понятие поля имеет глубокий физический смысл и что электромагнитное поле есть объективная реальность.
Согласно закону
Кулона, сила, действующая на «пробный»
заряд
,
при внесении его в поле других зарядов,
пропорциональна величине этого пробного
заряда
.
Поэтому силы электрического поля будут
вполне определены, если определена в
каждой точке этого поля сила, действующая
на помещенный в ней единичный положительный
заряд. Эта сила, действующая на заряд
,
называется напряженностью электрического
поля в данной точке:
(2.6)
Величина пробного
заряда
должна быть достаточно мала, чтобы этот
вносимый заряд не привел к перераспределению
зарядов на поверхностях и в объемах
заряженных тел, создающих исследуемое
электрическое поле. Измерив напряженность
в достаточно большом числе точек, мы
получим математическое поле
или
(
– точка пространства,
– ее радиус-вектор).
Так из закона
Кулона следует, что поле напряженности
неподвижного заряда
,
расположенного в начале координат имеет
вид
,
где
– радиус-вектор точки наблюдения,
– единичный вектор направления
.
Сила, действующая
на заряд
со стороны электрического поля, т.е.
сила действующая на неподвижный заряд
,
помещенный в точку с напряженностью
,
будет, очевидно, равна
. (2.7)
Для исследования и расчета электрического поля закон Кулона не всегда удобен, хотя он и является основным законом электростатики. Более удобной является теорема Гаусса.
Теорему Гаусса
можно вывести из закона Кулона. Она
гласит: для поля, созданного зарядами,
поток вектора напряженности электрического
поля
сквозь замкнутую поверхность
равен суммарному заряду, попавшему
внутрь
,
деленному на константу
:
.
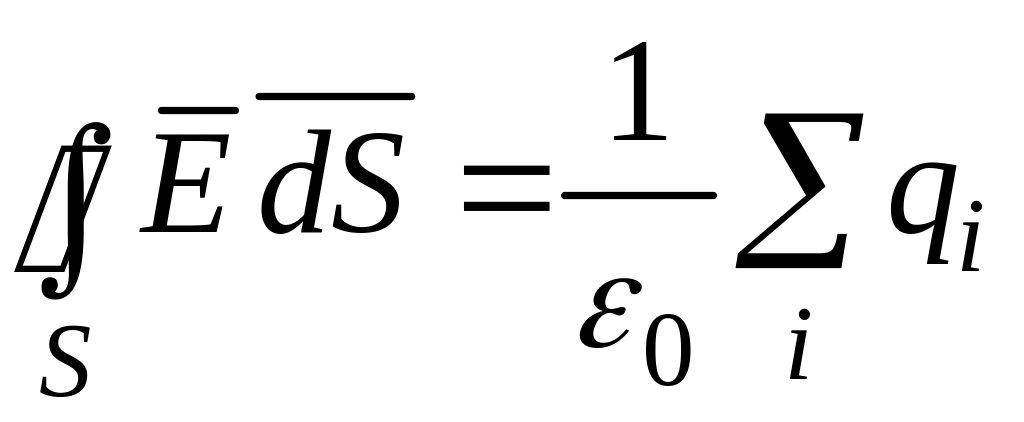(2.8)
В (2.8) суммируются
только заряды, находящиеся внутри
,
элемент
направлен во внешность замкнутой
поверхности
.
Например (рис. 2.2):
Рис. 2.2. Иллюстрация теоремы Гаусса в интегральной форме
.
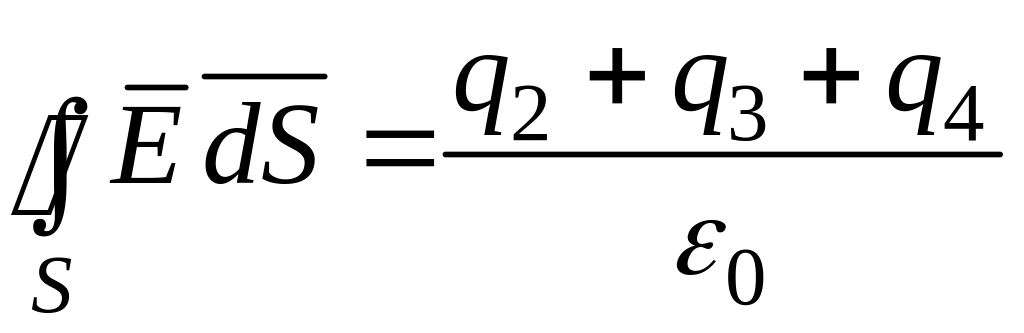Теорему Гаусса,
как и любой другой физический закон,
следует рассматривать как
причинно-следственную связь между
физическими величинами. Причина в (2.8)
стоит справа, т.е. электрические заряды,
которые порождают электрическое поле
– следствие, которое стоит слева
(сопоставьте в этом смысле теорему
Гаусса, например, со вторым законом
Ньютона в механике
).
В законе Кулона
(2.4) причиной являются заряды
,
,
которые также стоят справа, а следствием
является сила
или
,
которая стоит слева.
Из теоремы Гаусса можно вывести закон Кулона.
Если заряды распределены непрерывно («размазаны») в некоторой части пространства (рис. 2.3), то для характеристики интенсивности заряда в точке М вводится понятие плотности заряда (по аналогии с плотностью массы):
,
(2.9)
где
заряд внутри физически бесконечно-малого
объема
.
Рис. 2.3. К определению плотности заряда
При непрерывном распределении зарядов теорема Гаусса запишется так:
.
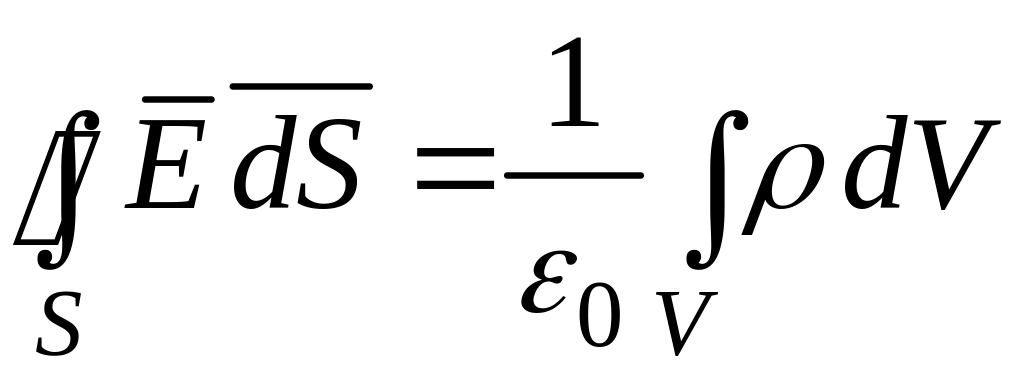(2.10)
Здесь
– замкнутая поверхность, ограничивающая
объем
.
Вектор
ориентирован изнутри наружу.