Задачи по непрерывным случайным величинам

Задача 1

Точка x наудачу бросается на отрезок [-8,8]. Найти:

1. 

2. 

Решение:

1. 

2. 

Задача 2

Пусть НСВ X распределена на отрезке [0, 6]? Её функция плотности . Найти:

1. 

2. 

3. 

4. 

5. =?

Решение:

1. 

2. 

3. 

4. 

5. 

Задача 3

Точка M наудачу бросается в окружность радиуса R=3. Пусть r – расстояние от точки M до центра окружность. Записать её интегральную функцию распределения .

Решение:

2 случая:

1. Если , то

2. Если , то:

Допустим, r=2, . Из этого делаем вывод, что

Задача 4

Пусть НСВ X распределена на отрезке [0, 5]. Её интегральная функция распределения . Найти:

2. 

3. 

Решение:

1. 

2. 

3. 

Задача 5

X . Пусть . Найти:

1. 

2. 

Решение:

1. 

Находим . 2 решения:

1. 3 случая:

1. Если x<1, то

2. Если x>5, то

3. Если , то:

Допустим, x=3. . Из этого делаем вывод, что

2. Т.к. X

2. 

Закон больших чисел. Неравенства Чебышёва, Маркова, Колмогорова

Неравенство Чебышева

Неравенство Чебышева даёт оценку вероятности того, что случайная величина в основном принимает значения, близкие к своему среднему.

Пусть случайная величина X имеет математическое ожидание М и дисперсию D. Тогда для любого 0 справедливо неравенство Чебышева

Теорема: Пусть НСВ. Тогда ,

Пример: Пусть x – НСВ. Плотность распределения .

Из неравенства Чебышева следует:

; ;

;

После подсчёта вероятности с помощью формулы Лапласа получились результаты:

; ;

;

Неравенство Маркова

Неравенство Маркова даёт оценку вероятности того, что случайная величина превзойдёт по модулю фиксированную положительную константу, в терминах её математического ожидания.

Теорема: Пусть НСВ. Тогда ,

Неравенство Колмогорова

Неравенство Колмогорова даёт оценку вероятности того, что частичная сумма конечной совокупности независимых случайных величин не превышает некоторого фиксированного числа.

Теорема: – последовательность независимых случайных величин таких, что . Тогда

,

Закон больших чисел

Определение: Пусть – последовательность независимых случайных величин. Данная последовательность подчиняется закону больших чисел, если среднее арифметическое этих случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий.

Примечание: Если – число успехов в i-том испытании по схеме Бернулли, то утверждение закона больших чисел совпадает с теоремой Бернулли.

Суть закона больших чисел состоит в том, что при возрастании числа слагаемых (т.е. одинаково распределенных случайных величин) среднее арифметическое этих слагаемых мало отличается от математического ожидания. Любое отклонение среднего арифметического случайных величин от математического ожидания при достаточно большом числе слагаемых – маловероятно.

Усиленный закон больших чисел

= 1, где

Центральная предельная теорема. Интегральная функция Муавра-Лапласа

Функция Лапласа

Свойства функции Лапласа:

1. Определена на всей оси

2. Множество её возможных значений

3. Возрастает

4. 

5. 

6. (причём, уже при можно считать, что )

Кривая Гаусса

Формула кривой Гаусса:

Здесь

Определение:

1. ДСВ X – величина нормального типа, если огибающая линия её графического изображения приблизительно совпадает с кривой Гаусса.

2. НСВ X – величина нормального типа, если её график плотности приблизительно совпадает с кривой Гаусса.

Центральная предельная теорема

Если случайная величина представляет собой сумму большого числа независимых случайных величин (т.е. , где n – большое число), то тогда эта величина будет иметь распределение близкое к нормальному (т.е. будет величиной нормального типа).

Пусть – сумма независимых реализаций величины x.

Тогда при распределение стремится к нормальному распределению.

Примечание: n должно быть настолько большим, чтобы соблюдались следующие условия:

Теорема (формула Лапласа): Пусть – величина нормального типа, тогда для расчёта вероятностей вида можно использовать приближённую формулу:

1. Если – целочисленная величина нормального типа, то

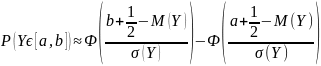
2. Если – нецелочисленная величина нормального типа, то

Теорема: Пусть – величина нормального типа, тогда величина с практически достоверной гарантией (99,9%) будет максимальна в диапазоне:

Этот диапазон называется зоной практического нахождения величины Y ( ЗПН( ) ).

Пример: Игральный кубик подбрасывается 1000 раз. Пусть – какая получится сумма возможных значений (характеристики случайной величины : . Найти:

1. Характеристики

2. Доказать, что – величина нормального типа

3. 

4. 

5. 

6. ЗПН( )

Решение:

, где x – сколько очков выпало на кубике при отдельном подбрасывании.

x			3			6
p

1. Чтобы найти характеристики нужно найти характеристики отдельно взятого слагаемого ( ).

Характеристики Y:

2. – величина нормального типа?

Верно ли, что ?

- Верно

Верно ли, что ?

– Верно

Условия выполнены, следовательно, Y – величина нормального типа, следовательно, для расчёта её вероятностей можно использовать формулу Лапласа.

3. 

4. 

5. 

=[3322, 3678]

Формулу Лапласа также можно применить и к НСВ.

Основные типы распределений НСВ

1. Равномерное распределение

2. Показательное распределение

3. Нормальное распределение

Пример равномерного распределения: На отрезок [0, 3] наудачу бросается 100 точек. Пусть . Найти:

1. Характеристики (min, max, M, D, σ)

2. Доказать, что – величина нормального типа

3. ЗПН( )

4. 

Решение:

1. 

2. – величина нормального типа?

?

- Верно

?

- Верно

следовательно, Z – величина нормального типа, следовательно, для расчёта её вероятностей можно использовать формулу Лапласа.

3. ЗПН( )

=[121,51; 178,49]

4. 

Для НСВ нормального типа в формуле Лапласа поправки не ставятся.

Пример показательного распределения: Пусть X имеет показательное распределение и . Найти:

1. 

2. 

3. 

4. 

Показательное распределение =>

Решение:

1. 

2. 

Пример нормального распределения: ; Y , X и Y – независимы. Найти

Решение: Пусть . – нормальная величина.

;