Минобрнауки России

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Национальный исследовательский университет Московский энергетический институт»

(ФГБОУ ВПО «НИУ МЭИ»)

Факультет «Институт экономической безопасности бизнеса» (ИЭББ)

Кафедра «Защита информации»

Реферат по дисциплине «Теория вероятностей» по темам:

«Дискретные случайные величины. Функция распределения дискретных случайных величин. Математическое ожидание и дисперсия дискретных случайных величин» «Непрерывные случайные величины. Функция распределения непрерывных случайных величин. Плотность распределения, математическое ожидание и дисперсия непрерывных случайных величин» «Закон больших чисел. Неравенства Чебышёва, Маркова, Колмогорова. Центральная предельная теорема. Интегральная функция Муавра-Лапласа»

Работу выполнил:

студент гр. ИБС 11-12

Будынков Алексей

Работу проверила:

Кленина Л.И

Оценка______________

Подпись______________

Москва 2013

Оглавлени

Дискретные случайные величины. Функция распределения дискретных случайных величин. Математическое ожидание и дисперсия дискретных случайных величин 3

Задачи по дискретным случайным величинам 6

Непрерывные случайные величины. Функция распределения непрерывных случайных величин. Плотность распределения, математическое ожидание и дисперсия непрерывных случайных величин 8

Задачи по непрерывным случайным величинам 13

Закон больших чисел. Неравенства Чебышёва, Маркова, Колмогорова 16

Центральная предельная теорема. Интегральная функция Муавра-Лапласа 18

Задачи На применение Интегральной функцит Муавра-Лапласа 23

Список литературы 26

Дискретные случайные величины. Функция распределения дискретных случайных величин. Математическое ожидание и дисперсия дискретных случайных величин……………………………………………………..3

Задачи по дискретным случайным величинам…………...6

Непрерывные случайные величины. Функция распределения непрерывных случайных величин. Плотность распределения, математическое ожидание и дисперсия непрерывных случайных величин…………8

Задачи по непрерывным случайным величинам……….13

Закон больших чисел. Неравенства Чебышёва, Маркова, Колмогорова……………………………………………………………….14

Центральная предельная теорема. Интегральная функция Муавра-Лапласа…………………………………………….18

Задачи На применение Интегральной функцит Муавра-Лапласа……………………………………………………………………….23

Список литературы……………………………………………………..26

Дискретные случайные величины. Функция распределения дискретных случайных величин. Математическое ожидание и дисперсия дискретных случайных величин

Определение: Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает некоторое одно значение из множества возможных значений.

Случайная величина характеризуется:

1. Множеством возможных значений;

2. Распределением вероятностей по этим возможным значениям.

Определение: Если множество возможных значений случайной величины представляет собой конечное множество или бесконечную последовательность , то такая случайная величина является дискретной (ДСВ).

ДСВ X считается заданной, если заданы все её возможные значения, а также вероятности, с которыми X может принимать эти значения.

Указанная перечень всех возможных значений ДСВ – распределение ДСВ. Оно оформляется в виде следующей таблицы:

x			…
p			…

При этом должно выполняться следующее равенство

Функция распределения ДСВ определяется по формуле:

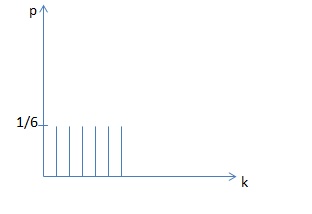
Пример: Подбрасывается игральный кубик. Пусть k – сколько очков выпадет на верхней грани. Записать распределение величины k.

x			3			6
p

Сделаем диаграмму случайных величин.

Математическое ожидание ДСВ

Определение: Пусть ДСВ X имеет следующую таблицу распределения:

x			…
p			…

Математическим величины X (обозначение: ) называется число:

Математическое ожидание выражает центр тяжести случайной величины.

Свойства математического ожидания:

1. ;

2. Пусть X имеет распределение:

x			…
p			…

Пусть от X берётся функция f(x), тогда

Например:

Примечание: В общем случае

3. Пусть c – константа, тогда:

   1. 

   2. 

4. 

Примечание: Свойство 4 верно как для независимых, так и для зависимых величин.

5. Если x и y независимы, то

6. 

Примечание: Если X – бесконечная ДСВ (то есть, множество её возможных значений бесконечно), то определяется суммой числового ряда , при условии, что ряд абсолютно сходится. В противном случае говорят, что не существует.

Дисперсия ДСВ

Определение: Дисперсией случайной величины X (обозначение: ) называется число:

Дисперсия выражает меру рассеяния случайной величины относительно своего математического ожидания. Чем плотнее сгруппирована случайная величина относительно своего математического ожидания, тем меньше дисперсия.

Свойства дисперсии:

1. Для любой величины

2. 

3. Пусть c – константа, тогда

4. Пусть c – константа, тогда

5. Если x и y независимы, то:

   1. 

   2. 

6. Пусть x и y независимы и пусть для каждой из них известны математическое ожидание и дисперсия, тогда можно найти дисперсию x*y.

(их мы находим по второму свойству)