Система уравнений первого порядка и структура матриц коэффициентов для анизотропных сред тригональной сингонии
Для тригональной сингонии класса 3 явный вид дифференциальных уравнений 1-го порядка:
(2.2.1)
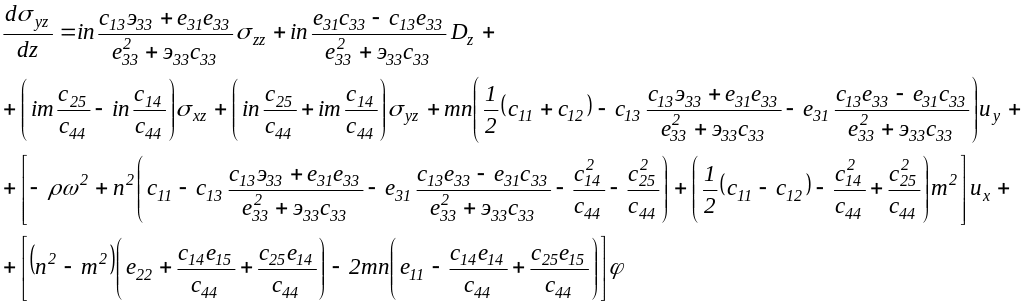
Для пьезокристаллов тригональной сингонии класса 3 структура матрицы В имеет вид:
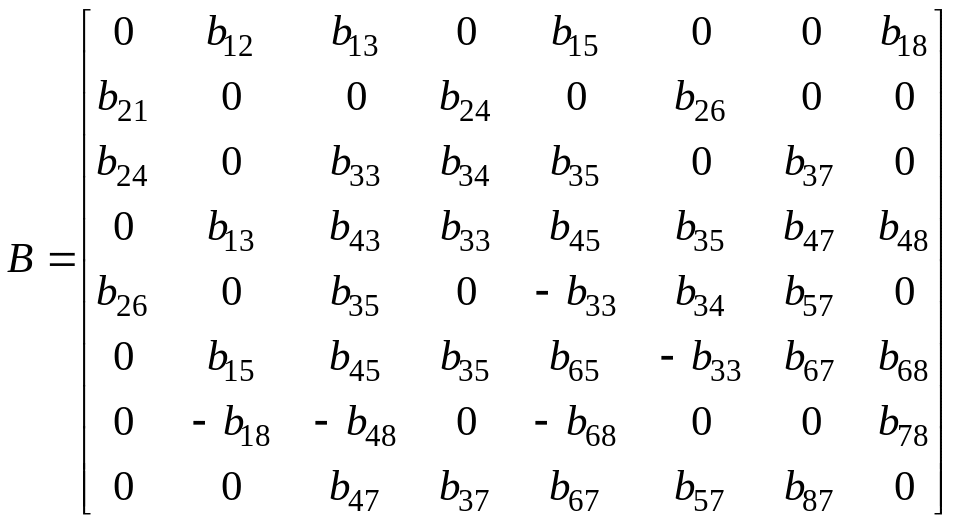(2.2.2)
Из (2.2.2) следуют структуры матриц коэффициентов при распространении волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz)
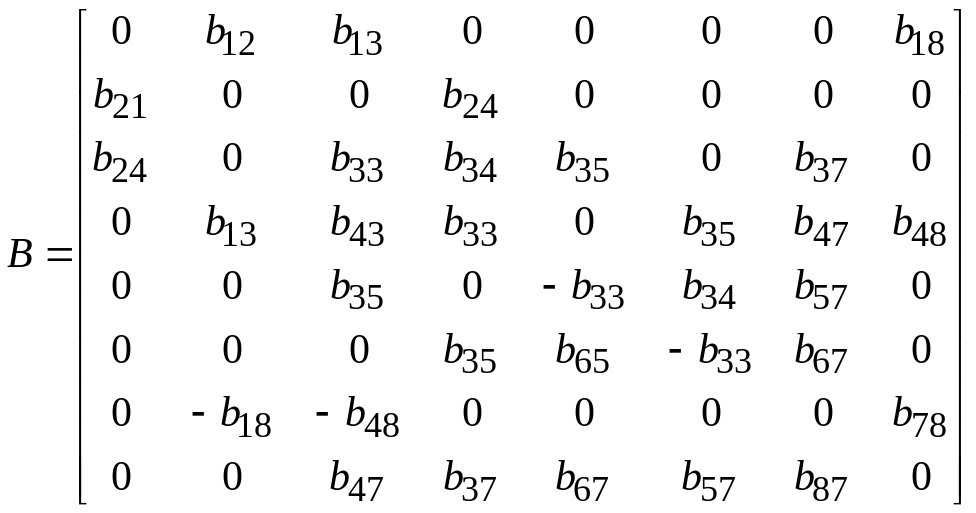(2.2.3)
Из структуры данной матрицы видно, что все волны распространяются связанно. Продольная волна является упругой и связана с поперечной х-поляризованной пьезоупругой волной. Поперечная х-поляризованная пьезоупругая и поперечная у-поляризованная упругая волны также связаны друг с другом.
б) плоскость (yz)
(2.2.4)
Из структуры данной матрицы видно, что все волны также взаимосвязаны. Так, продольная упругая волна связана с поперечной у-поляризованной пьезоупругой. Поперечная х-поляризованная упругая и поперечная у-поляризованная пьезоупругая волны также распространяются связанно.
Для тригональной сингонии класса 32 явный вид дифференциальных уравнений 1-го порядка: [134, С.15]
(2.2.5)
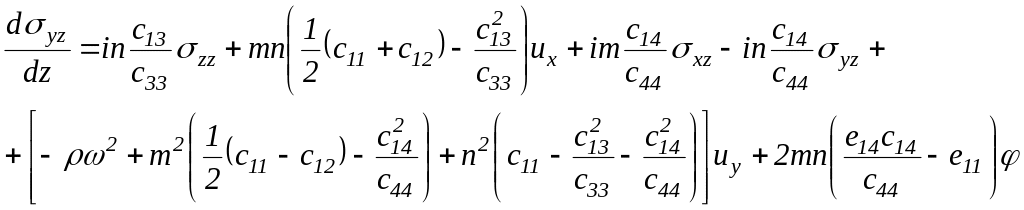
Для пьезокристаллов тригональной сингонии класса 32 структура матрицы В имеет вид:
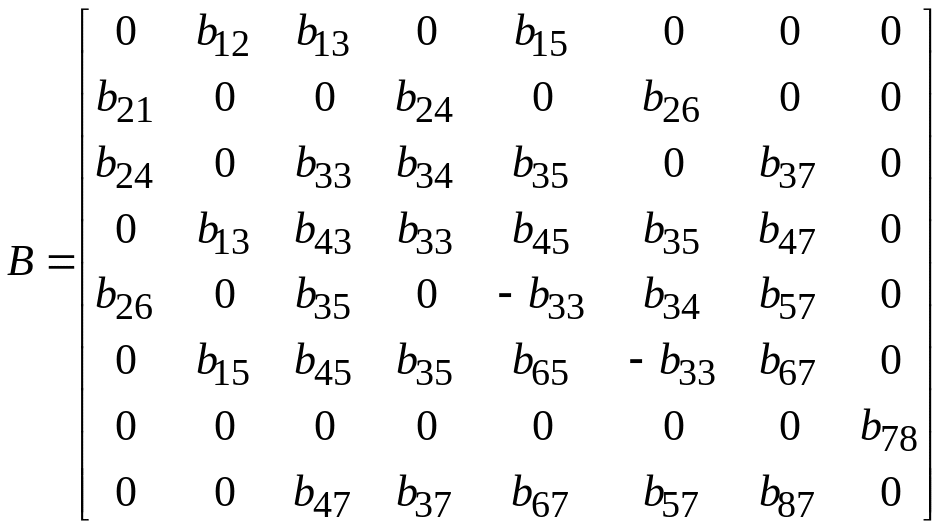
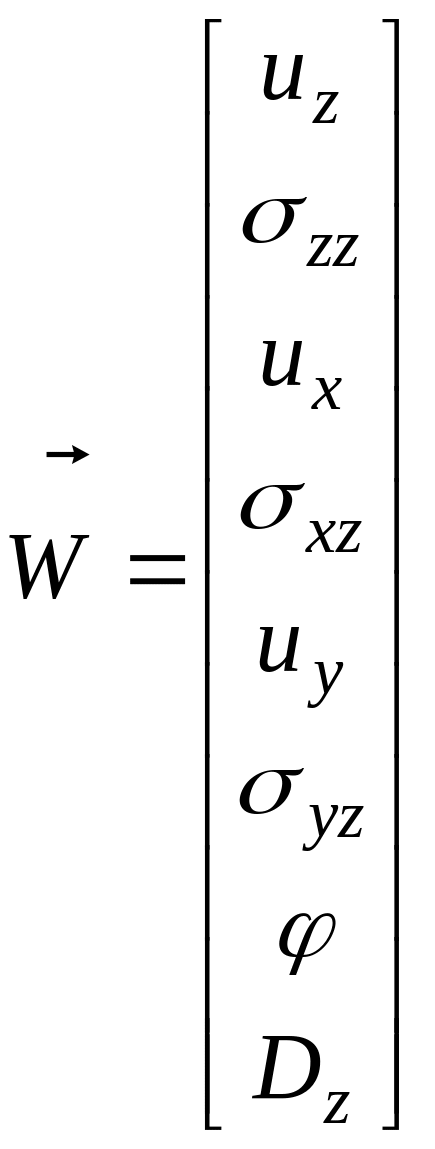(2.2.6)
Из (2.2.6) следуют структуры матриц коэффициентов при распространении волн в координатных плоскостях.
а) плоскость (xz)
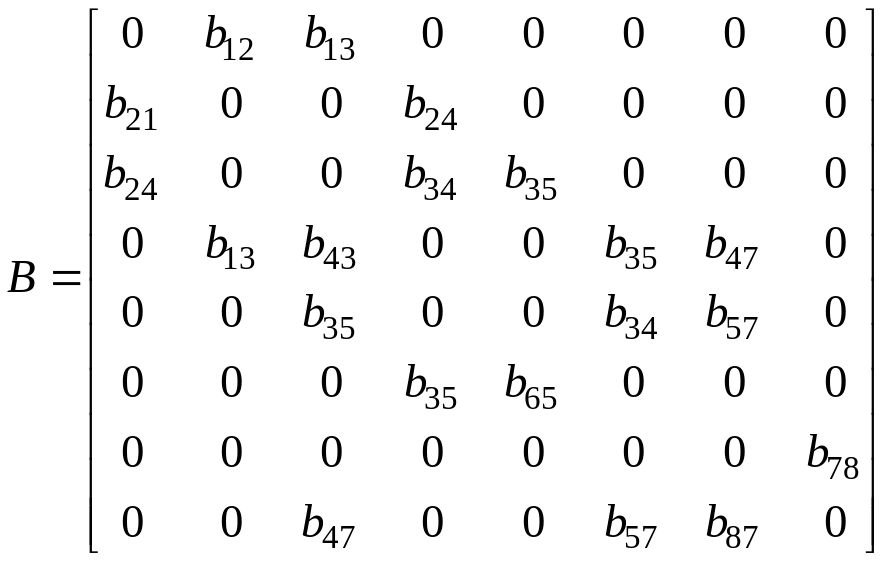(2.2.7)
Данная матрица
описывает распространение связанных
продольной упругой и поперечных
электроупругих волн х
и у
поляризации. Коэффициенты
и
осуществляют связь между продольной и
поперечной х-поляризованной
упругими волнами, коэффициенты
и
связывает поперечные упругие волны х
и у
поляризации. Связь же с электрическим
полем поперечных
упругих волн х
и у
поляризации осуществляют соответственно
коэффициенты
и
.
б) плоскость (yz)
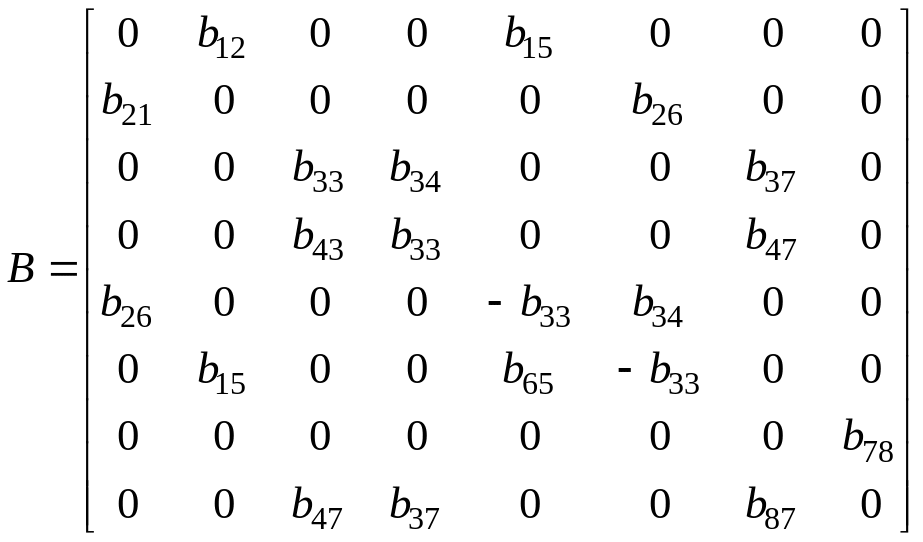(2.2.8)
Данная
структура показывает, что поперечная
х-поляризованная
волна распространяется независимо от
других волн и является электроупругой,
так как связана с электрическим полем
коэффициентами
и
,
которые содержат в себе пьезоупругие
постоянные. А продольная и поперечная
у-поляризованная
волны связаны коэффициентами
и
,
и являются упругими, поскольку содержат
в себе упругие постоянные. Наличие
отличных от нуля диагональных элементов
говорит о перекачке энергии между
волнами различной поляризации.
Для тригональной сингонии класса 3m явный вид дифференциальных уравнений 1-го порядка:
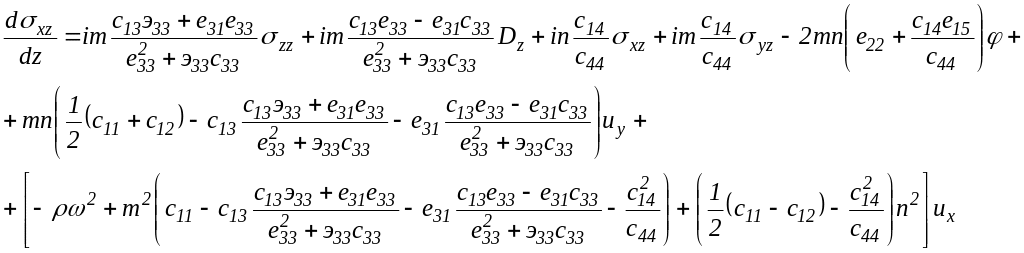
(2.2.9)
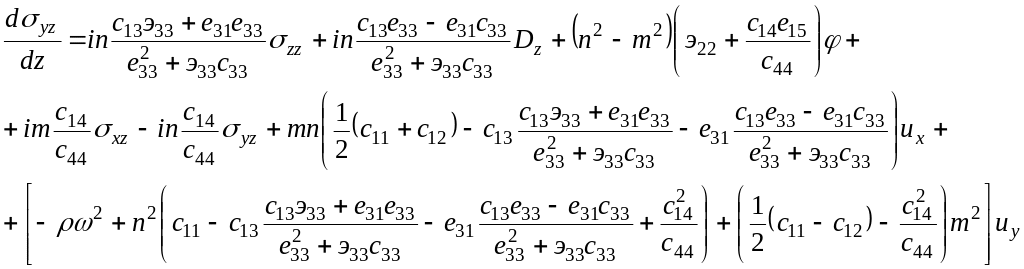
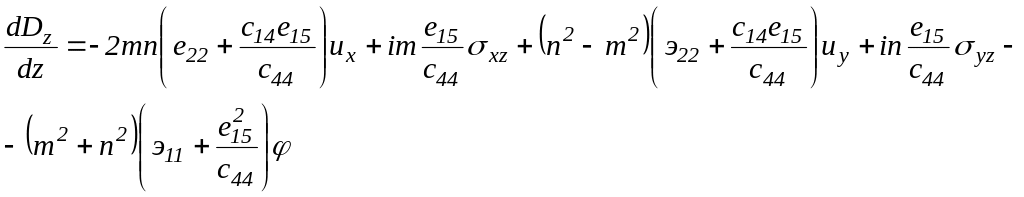
Для пьезокристаллов тригональной сингонии класса 3m структура матрицы В имеет вид:[128, С.124]
(2.2.10)
Из (2.2.10) следуют структуры матриц коэффициентов при распространении волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz)
(2.2.11)
Из структуры данной матрицы видно, что продольная и поперечная х-поляризованная волны связаны и являются пьезоупругими. А поперечные х и у-поляризованные волны являются электроупругими и распространяются связанно. Все волны связаны с электрическим полем.
б) плоскость (yz)
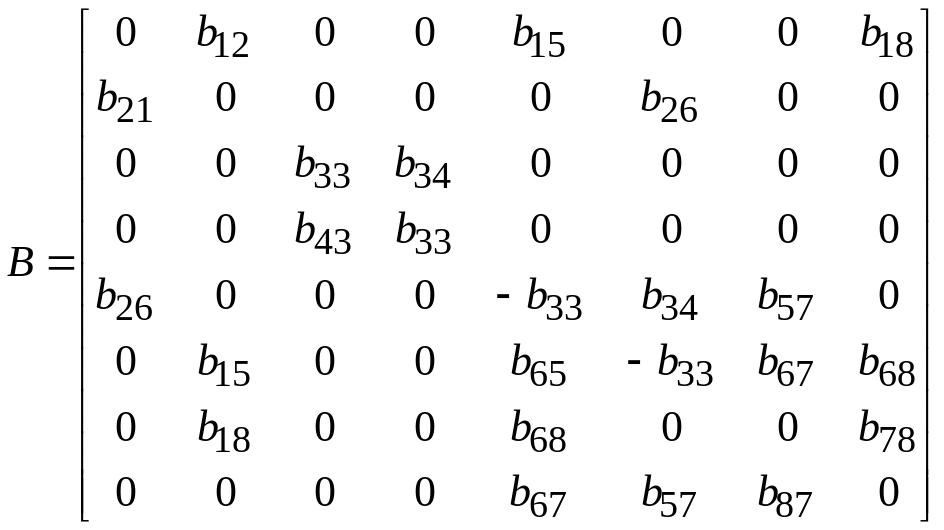(2.2.12)
Данная структура показывает, что упругая х-поляризованная поперечная волна распространяется независимо. А продольная и поперечная у-поляризованная волны связаны и являются электроупругими.