2 Построение систем дифференциальных уравнений первого порядка
В данном разделе в квазистатическом приближении рассматривается построение систем дифференциальных уравнений первого порядка и определены структуры матриц коэффициентов для объемных (как частный случай, плоских) пьезоупругих волн распространяющихся в анизотропных средах кубической, гексагональной, тетрагональной, ромбической и тригональной сингоний, неоднородных вдоль одной из пространственных координат. Приведен анализ полученных матриц, определены типы волн распространяющихся в данных средах, взаимосвязь между ними и потенциальным электрическим полем.
Система уравнений первого порядка и структура матриц коэффициентов для анизотропных сред кубической, гексагональной, тетрагональной и ромбической сингоний
Построение систем
дифференциальных уравнений первого
порядка основывается на сведении к ним
исходных уравнений для вектора смещения
и электрического
потенциала
(1.3.4),
описывающих динамику исследуемого
волнового процесса, с учетом (1.3.3) методом
разделения переменных. В случае
гармонических волн решение можно
представить в виде:
При неоднородности среды вдоль оси z, которая совмещена с осью симметрии кристалла, из системы уравнений выделяются производные по z и исключаются, не входящие в граничные условия компоненты тензора напряжений и электрического поля.
Полученная система
дифференциальных уравнений первого
порядка, относительно вектора
,
описывающая распространение гармонических
волн
может быть
записана в матричной форме:[112,149]
(2.1.1)
Вектор имеет вид
(2.1.2)
Множитель
далее опущен. Символ
означает операцию транспонирования
вектора - строки в вектор – столбец,
–
компоненты вектора смещения и тензора
напряжения,
–
компонента вектора электрического
смещения,
– электрический потенциал,
– круговая частота,
– компоненты волнового вектора
вдоль осей x
и y.
Элементы матрицы коэффициентов содержат в себе параметры среды, в которой распространяется пьезоупругая волна.
(2.1.3)
Поэтому знание структуры В позволяет говорить о типах волн распространяющихся в данной анизотропной среде и связях между ними.
Анализ структуры матрицы коэффициентов проводится следующим образом:
Для анизотропной среды строится система дифференциальных уравнений первого порядка (2.1.2);
Определяется структура матрицы коэффициентов в объемном случае распространения;
Полагая равными нулю соответствующие компоненты волнового вектора , определяются матрицы коэффициентов, описывающих распространение волны в координатных плоскостях;
Рассматриваются волны, распространяющиеся в данной среде:
Элементы
и
описывают распространение продольной
упругой волны;Элементы
и
описывают распространение поперечной
упругой х-поляризованной
волны;Элементы
и
описывают распространение поперечной
упругой у-поляризованной
волны;Элементы
и
характеризуют потенциальное электрическое
поле;
Другие ненулевые элементы осуществляют связь между этими волнами и потенциальным электрическим полем.
В случае
распространения волн в анизотропной
среде
кубической
сингонии классов 23 и
явный вид дифференциальных уравнений
первого порядка (2.1.1) имеют следующий
вид:
(2.1.4)
Из этой системы уравнений первого порядка можно определить структуру матрицы коэффициентов. Она имеет следующий вид:
(2.1.5)
Из (2.1.5) следуют структуры матриц коэффициентов при распространении волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz)
(2.1.6)
Из структуры данной матрицы видно, что она разделяется на две независимые матрицы четвертого порядка. Первая описывает распространение связанных продольной и поперечной х-поляризованной упругих волн. Вторая – пьезоупругую поперечную у-поляризованную волну.
б) плоскость (yz)
(2.1.7)
Данная матрица описывает распространение связанных продольной и поперечной у-поляризованной упругих волн, а также независимую пьезоупругую поперечную х-поляризованную волну.
Для гексагональной сингонии класса 6 явный вид дифференциальных уравнений первого порядка:
(2.1.8)
Для пьезокристаллов гексагональной сингонии класса 6 структура матрицы В имеет вид: [127, С.202]
(2.1.9)
Из (2.1.9) следуют структуры матриц коэффициентов при распространении пьезоупругих волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz) (n=0):
(2.1.10)
Из структуры данной матрицы видно, что продольная и поперечная х-поляризованная волны связаны и являются пьезоупругими. А поперечная у-поляризованная волна распространяется независимо и является упругой. Все волны связаны с электрическим полем.
б) плоскость (yz) (m=0):
(2.1.11)
Из структуры данной матрицы видно, что продольная и поперечная у-поляризованная волны связаны и являются пьезоупругими. А поперечная х-поляризованная волна распространяется независимо и является упругой. Все волны связаны с электрическим полем.
Для гексагональной
сингонии класса
явный
вид дифференциальных уравнений 1-го
порядка:
(2.1.12)
Для пьезокристаллов
гексагональной сингонии класса
структура
матрицы В
имеет вид:
(2.1.13)
Из (2.1.13) следуют структуры матриц коэффициентов при распространении пьезоупругих волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz) (n=0):
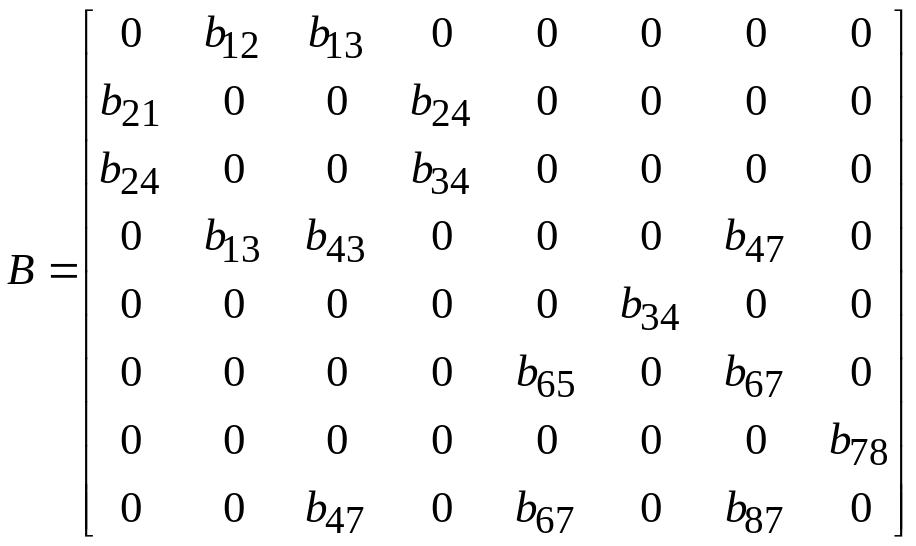(2.1.14)
Из структуры данной матрицы видно, что продольная и поперечная х-поляризованная волны связаны и являются упругими. А поперечная у-поляризованная волна распространяется независимо и является упругой. Все волны связаны с электрическим полем.
б) плоскость (yz) (m=0):
(2.1.15)
Из структуры данной матрицы видно, что продольная и поперечная у-поляризованная волны связаны и являются упругими. А поперечная х-поляризованная волна распространяется независимо и является упругой. Все волны связаны с электрическим полем.
Для гексагональной сингонии класса 622 явный вид дифференциальных уравнений первого порядка:
(2.1.16)
Для пьезокристаллов гексагональной сингонии класса 622 структура матрицы В имеет вид: [127, С.203]
(2.1.17)
Из (2.1.17) следуют структуры матриц коэффициентов при распространении пьезоупругих волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz) (n=0):
(2.1.18)
Из структуры данной матрицы видно, что она разделяется на две независимые матрицы четвертого порядка. Первая описывает распространение связанных продольной и поперечной х-поляризованной упругих волн. Вторая – независимую пьезоупругую поперечную у-поляризованную волну.
б) плоскость (yz) (m=0):
(2.1.19)
Данная матрица описывает распространение связанных продольной и поперечной у-поляризованной упругих волн, а также независимую пьезоупругую поперечную х-поляризованную волну.
Для гексагональной сингонии класса 6mm явный вид дифференциальных уравнений первого порядка:
(2.1.20)
Для пьезокристаллов гексагональной сингонии класса 6mm структура матрицы В имеет вид:
(2.1.21)
Из (2.1.21) следуют структуры матриц коэффициентов при распространении пьезоупругих волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz) (n=0):
(2.1.22)
Данная структура показывает, что упругая у-поляризованная поперечная волна распространяется независимо. А продольная и поперечная х-поляризованная волны связаны и являются электроупругими.
б) плоскость (yz) (m=0):
(2.1.23)
Данная структура показывает, что упругая х-поляризованная поперечная волна распространяется независимо. А продольная и поперечная у-поляризованная волны связаны и являются электроупругими.
Для
гексагональной
сингонии класса
явный
вид дифференциальных уравнений 1-го
порядка:
(2.1.24)
Для пьезокристаллов
гексагональной сингонии класса
структура
матрицы В
имеет вид:
(2.1.25)
Из (2.1.25) следуют структуры матриц коэффициентов при распространении пьезоупругих волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz) (n=0):
(2.1.26)
Данная структура показывает, что у-поляризованная упругая поперечная волна распространяется независимо и связана с электрическим полем. А продольная и поперечная х-поляризованная волны связаны и являются упругими.
б) плоскость (yz) (m=0):
(2.1.27)
Данная структура показывает, что х-поляризованная упругая поперечная волна распространяется независимо и связана с электрическим полем, а продольная и поперечная у-поляризованная волны связаны и являются упругими.
Для тетрагональной сингонии класса 4 явный вид дифференциальных уравнений 1-го порядка:[127]
(2.1.28)
Для пьезокристаллов тетрагональной сингонии класса 4 структура матрицы В имеет вид:
(2.1.29)
Из (2.1.29) следуют структуры матриц коэффициентов при распространении волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz) (n=0)
(2.1.30)
Из структуры данной матрицы видно, что продольная и поперечная х-поляризованная волны связаны и являются пьезоупругими. А поперечные х и у-поляризованные волны являются пьезоупругими и распространяются связанно.
б) плоскость (yz) (m=0)
(2.1.31)
Из структуры данной матрицы видно, что продольная и поперечная у-поляризованная волны связаны и являются пьезоупругими. А поперечные х и у-поляризованные волны являются пьезоупругими и распространяются связанно.
Для
тетрагональной сингонии класса
явный
вид дифференциальных уравнений 1-го
порядка: [127]
(2.1.32)
Из этой системы уравнений 1 –го порядка можно определить структуру матрицы коэффициентов. Она имеет следующий вид:
(2.1.33)
Из (2.1.33) следуют структуры матриц коэффициентов при распространении волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz) (n=0)
(2.1.34)
Из структуры данной матрицы видно, что продольная упругая и поперечная х-поляризованная пьезоупругая волны связаны. А поперечные х и у-поляризованные волны являются пьезоупругими и распространяются связанно.
б) плоскость (yz) (m=0)
(2.1.35)
Из структуры данной матрицы видно, что продольная упругая и поперечная у-поляризованная пьезоупругая волны связаны. А поперечные х и у-поляризованные волны являются пьезоупругими и распространяются связанно.
Для тетрагональной сингонии класса 422 явный вид дифференциальных уравнений 1-го порядка:[127]
(2.1.36)
Путем выше указанных преобразований получим следующую структуру матрицы коэффициентов:
(2.1.37)
Из (2.1.37) следуют структуры матриц коэффициентов при распространении волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz) (n=0)
(2.1.38)
Из структуры данной матрицы видно, что она разделяется на две независимые матрицы четвертого порядка. Первая описывает распространение связанных продольной и поперечной х-поляризованной упругих волн. Вторая – пьезоупругую поперечную у-поляризованную волну.
б) плоскость (yz) (m=0)
(2.1.39)
Данная матрица описывает распространение связанных продольной и поперечной у-поляризованной упругих волн, а также пьезоупругую поперечную х-поляризованную волну.
Для тетрагональной сингонии класса 4mm явный вид дифференциальных уравнений 1-го порядка:
(2.1.40)
Для пьезокристаллов тетрагональной сингонии класса 4mm структура матрицы В имеет вид: [127, С.200]
(2.1.41)
Из (2.1.41) следуют структуры матриц коэффициентов при распространении пьезоупругих волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz) (n=0):
(2.1.42)
Данная структура показывает, что упругая у-поляризованная поперечная волна распространяется независимо. А продольная и поперечная х-поляризованная волны связаны и являются электроупругими.
б) плоскость (yz) (m=0):
(2.1.43)
Данная структура показывает, что упругая х-поляризованная поперечная волна распространяется независимо. А продольная и поперечная у-поляризованная волны связаны и являются электроупругими.
Для
тетрагональной сингонии класса
явный
вид дифференциальных уравнений 1-го
порядка:
(2.1.44)
Из этой системы уравнений 1 –го порядка можно определить структуру матрицы коэффициентов. Она имеет следующий вид: [127, С.201]
(2.1.45)
Из (2.1.45) следуют структуры матриц коэффициентов при распространении волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz)
(2.1.46)
Из структуры данной матрицы видно, что она разделяется на две независимые матрицы четвертого порядка. Первая описывает распространение связанных продольной и поперечной х-поляризованной упругих волн. Вторая – пьезоупругую поперечную у-поляризованную волну.
б) плоскость (yz)
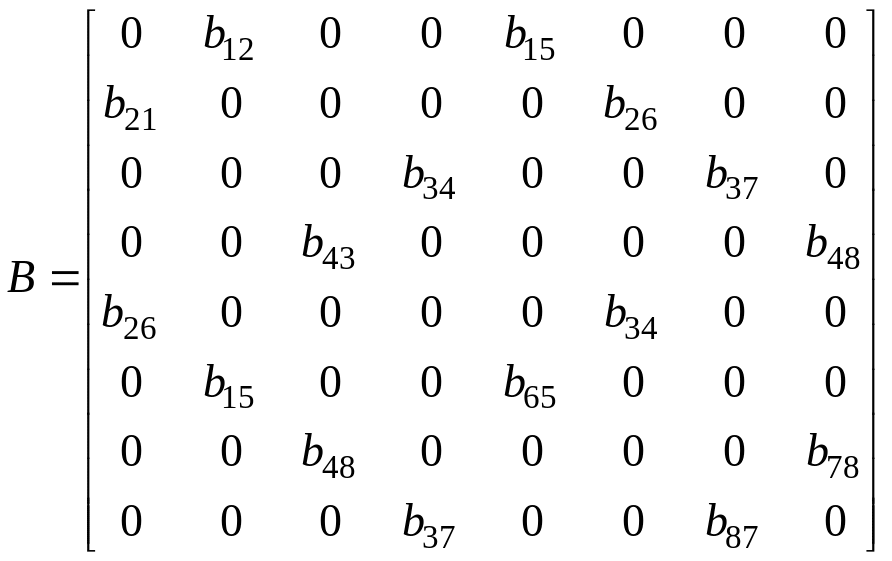(2.1.47)
Данная матрица описывает распространение связанных продольной и поперечной у-поляризованной упругих волн, а также независимую пьезоупругую поперечную х-поляризованную волну.
Для волн распространяющихся в средах ромбической сингонии класса 222 явный вид системы уравнений первого порядка имеет вид:
(2.1.48)
Из этой системы уравнений первого порядка можно определить структуру матрицы коэффициентов. Она имеет следующий вид: [130, С.158]
(2.1.49)
Из (2.1.49) следуют структуры матриц коэффициентов при распространении волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz)
(2.1.50)
Из структуры (2.1.50) видно, что матрица разделяется на две независимые друг от друга матрицы 4-го порядка. Первая описывает распространение связанных упругих продольной и поперечной х-поляризованной волн. Вторая описывает распространение электроупругой поперечной волны у-поляризации.
б) плоскость (yz)
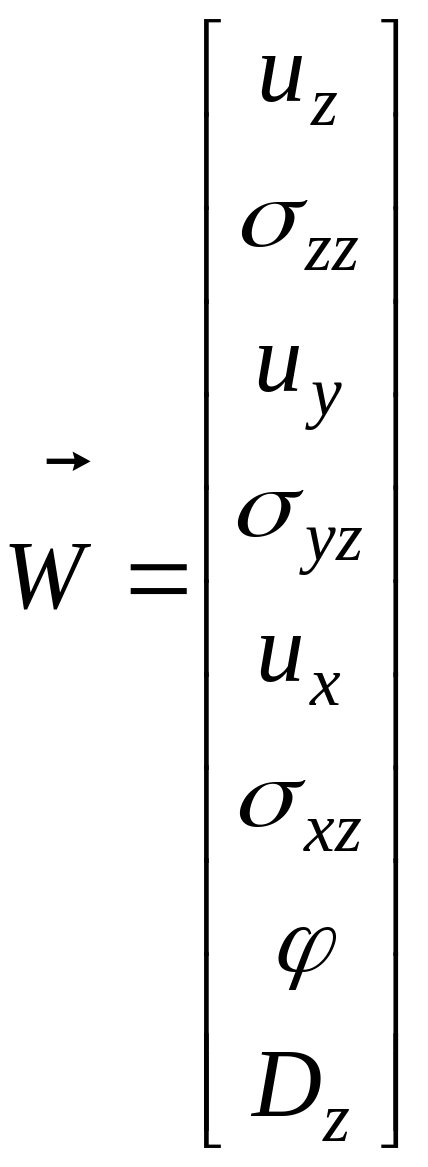(2.1.51)
Структура (2.1.51) показывает, что в плоскости (yz) распространяются связанные упругие продольная и поперечная у-поляризованная волны, и независимая поперечная волна х-поляризации, связанная с пьезоэффектом.
Для ромбической сингонии класса mm2 явный вид дифференциальных уравнений первого порядка:
(2.1.52)
Для пьезокристаллов ромбической сингонии класса mm2 структура матрицы В имеет вид: [130, С.159]
(2.1.53)
Из (2.1.53) следуют структуры матриц коэффициентов при распространении пьезоупругих волн в координатных плоскостях, которые имеют вид:
а) плоскость (xz) (n=0):
(2.1.54)
Из структуры (2.1.54) видно, что продольная и поперечная х-поляризованная волны связаны и обладают пьезоэффектом. Поперечная у-поляризованная волна распространяется независимо и является упругой.
б) плоскость (yz) (m=0):
(2.1.55)
Из структуры (2.1.55) видно, что продольная и поперечная у-поляризованная волны связаны и обладают пьезоэффектом. Поперечная х-поляризованная волна распространяется независимо и является упругой.