В гексагональной сингонии имеется шестикратная ось поворота или инверсии.

Класс 6 имеет шестикратную ось параллельную оси z матрица коэффициентов c_ijkl имеет вид:

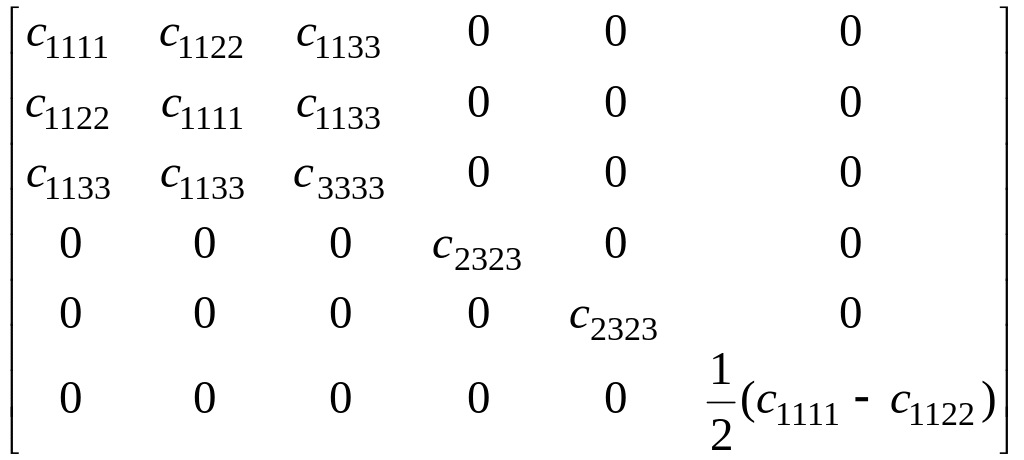(1.1.3)

Класс (шестикратная ось параллельна оси z) содержит трехкратную ось и признаки, характеризующие моноклинную систему класса m с плоскостью симметрии xy. Матрица коэффициентов c_ijkl не отличается от коэффициентов класса 6 (1.1.3).

Класс 622 имеет шестикратную ось поворота (параллельную оси z) и черты ромбической сингонии класса 222. Матрица коэффициентов c_ijkl не отличается от коэффициентов класса 6 (1.1.3).

Класс 6mm имеет шестикратную ось поворота (параллельную оси z) и признаки ромбической сингонии класса mm2. Матрица величин c_ijkl остается без изменения.

Класс объединяет в себе черты гексагональной системы класса и моноклинной системы класса 2 с двукратной осью симметрии, параллельной оси y. Матрица величин c_ijkl остается без изменения.

Кубическая сингония характеризуется четырьмя осями тройной симметрии, расположенными как диагонали в кубе.

Классы 23 и . Первая из этих систем объединяет в себе черты ромбической сингонии класса 222 и имеет четыре оси трехкратного поворота, расположенные вдоль диагоналей куба. В результате получаем следующую матрицу коэффициентов:

(1.1.4)

Тетрагональная сингония характеризуется четырехкратной осью поворота.

Класс 4 имеет четырехкратную ось симметрии, параллельную оси z. Вследствие влияния симметрии кристалла число независимых компонент тензоров c_ijkl сокращается до 6. Матрицы упругих параметров имеют вид:

(1.1.5)

Класс характеризуется четырехкратной осью инверсии, параллельной оси z. Произведем поворот системы координат на 90⁰ вокруг оси z, а затем инверсию. Тогда матрица коэффициентов c_ijkl не изменяется.

Класс 422 характеризуется четырехкратной осью симметрии, параллельной оси z. Коэффициенты материальных параметров среды должны одновременно определяться тетрагональной системой класса 4 и ромбической класса 222.

Тогда материальные параметры среды будут иметь следующий вид:

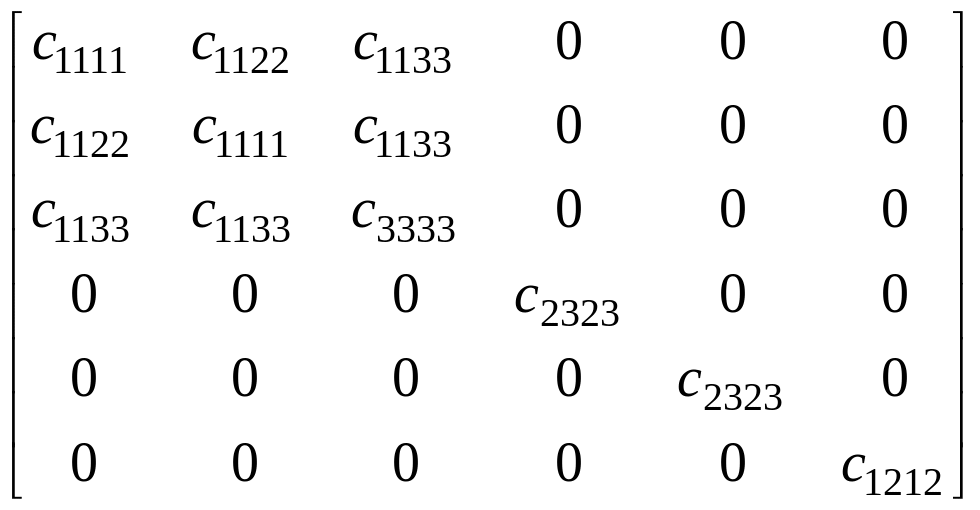(1.1.6)

Класс 4mm имеет четырехкратную ось поворота, параллельную оси z, и признаки, описывающие ромбическую сингонию класса mm2. Коэффициенты матрицы должны удовлетворять условиям тетрагональной сингонии класса 4 и ромбической сингонии класса mm2. В результате матрица коэффициентов c_ijkl не изменяется.

Класс объединяет в себе черты тетрагональной сингонии класса и ромбической сингонии класса 222. В результате матрица коэффициентов c_ijkl не изменяется.

Тригональная сингония имеет одну ось трехкратного поворота или инверсии.

Класс 3 имеет трехкратную ось, параллельную оси z. Матрицы материальных коэффициентов имеют вид:

(1.1.7)

Класс 32 с трехкратной осью, параллельной оси z, имеет в то же время черты, характерные для моноклинной системы с двукратной осью, параллельной оси x. В этом случае коэффициенты должны удовлетворять условиям симметрии обеих систем; отсюда следует возможность сокращения числа коэффициентов. Матрицы коэффициентов имеют вид:

(1.1.8)

Класс 3m имеет трехкратную ось, параллельную оси z, и черты, характерные для моноклинной системы с плоскостью симметрии yz. Матрица коэффициентов c_ijkl не изменяется и имеет вид (1.1.8).