5 Однородные анизотропные пьезодиэлектрики
В данном разделе строится структура усредненного матрицанта, на основе которого строятся уравнения дисперсии для однородного слоя при различных граничных условиях. Рассматривается построение уравнений индикатрис скоростей двумерных пьезоупругих волн, распространяющихся в анизотропных средах ромбической, кубической, тетрагональной и гексагональной сингоний. Графически построены сечения поверхности скоростей двумерных пьезоупругих волн для данных сред.
5.1 Матрицант однородной анизотропной среды в явной аналитической форме. Уравнения дисперсии пьезоупругих волн в однородном слое при различных граничных условиях
Уравнения дисперсии пьезоупругих волн в однородном слое строятся на основе однородного уравнения:
(5.1.1)
где
-
вектор начальных условий.
Построим уравнения дисперсии в однородном слое для волн распространяющихся в среде ромбической сингонии класса mm2.
Структуру
можно получить на основе представления
матрицанта уравнений движения для
усредненной среды, который в явной
аналитической форме имеет вид (4.2.8):
[135,C.53]
где Е-единичная матрица, - усредненная матрица коэффициентов
Для получения
структуры усредненного матрицанта
необходимо знание структуры матрицы
коэффициентов В
и структуру некоторой матрицы
,
которые в случае распространения в
плоскости (yz)
пьезоупругой волны в среде ромбической
сингонии класса mm2
имеют вид (3.1.4)
и (4.2.5):
Введем некоторые обозначения:
Итак, структура усредненного матрицанта имеет вид: [135,C.53]
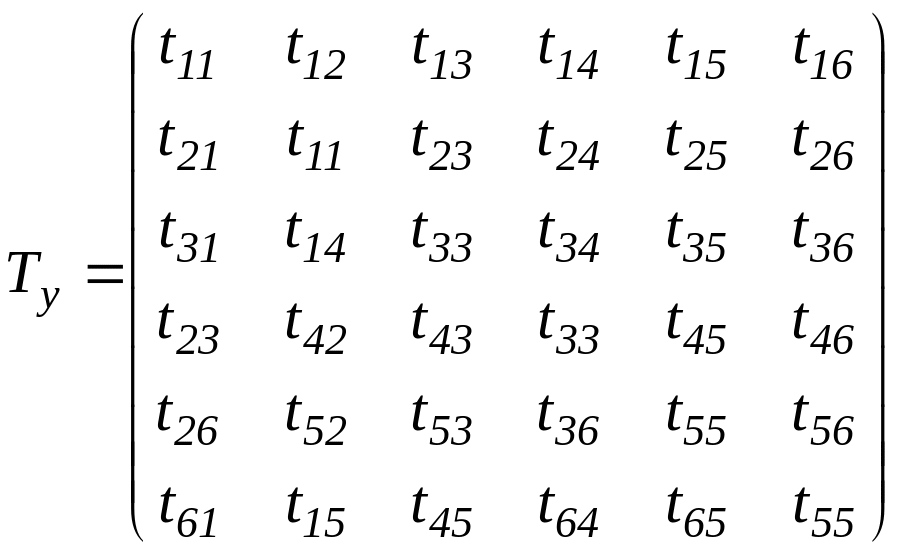(5.1.2)
Элементы
можно записать как
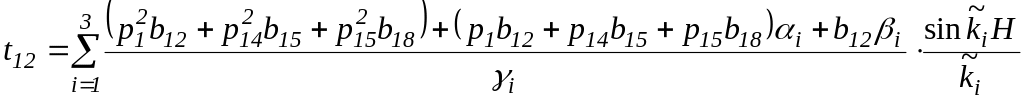
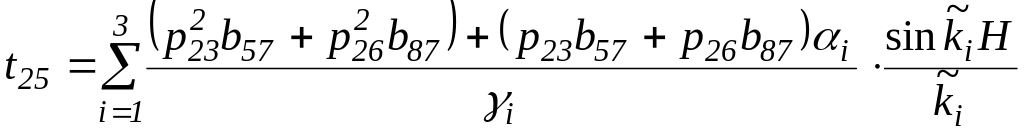
(5.1.3)
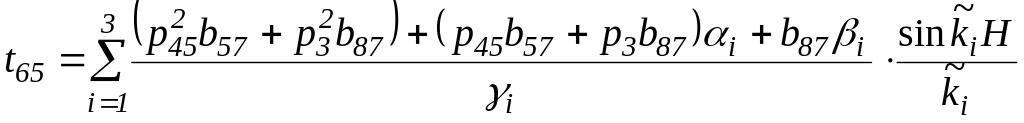
Получим уравнения дисперсии пьезоупругих волн при различных граничных условиях. Граничные условия для свободных и металлизированных границ слоя записываются в виде: [12]
(5.1.4)
т.е. на границах слоя примем равными нулю компоненты тензора напряжений и электрического потенциала.
Уравнение дисперсии определяется из (5.1.1) с учетом (5.1.4) из соотношения:
Это уравнение приводит к алгебраической системе однородных уравнений
Условием существования нетривиальных решений является равенство нулю детерминанта
(5.1.5)
Если границы слоя жестко закреплены и металлизированы, то:
(5.1.6)
т.е. на границах слоя смещение и электрический потенциал равны нулю.
Уравнение дисперсии следует из соотношения:
(5.1.7)
Когда границы свободно – жестко закреплены и металлизированы, то
(5.1.8)
В этом случае толщина слоя жестко закреплена и на границах слоя электрический потенциал равен нулю.
(5.1.9)
Подстановка элементов tij из (5.1.3) в уравнения (5.1.5), (5.1.7) и (5.1.9) дает уравнения дисперсии пьезоэлектрических волн в явной аналитической форме.
Построим уравнения дисперсии в однородном слое для волн распространяющихся в среде ромбической сингонии класса 222 (плоскость xz).
Структура усредненного матрицанта строится на основе аналитического представления (4.2.12):
и имеет вид [131,C.294]
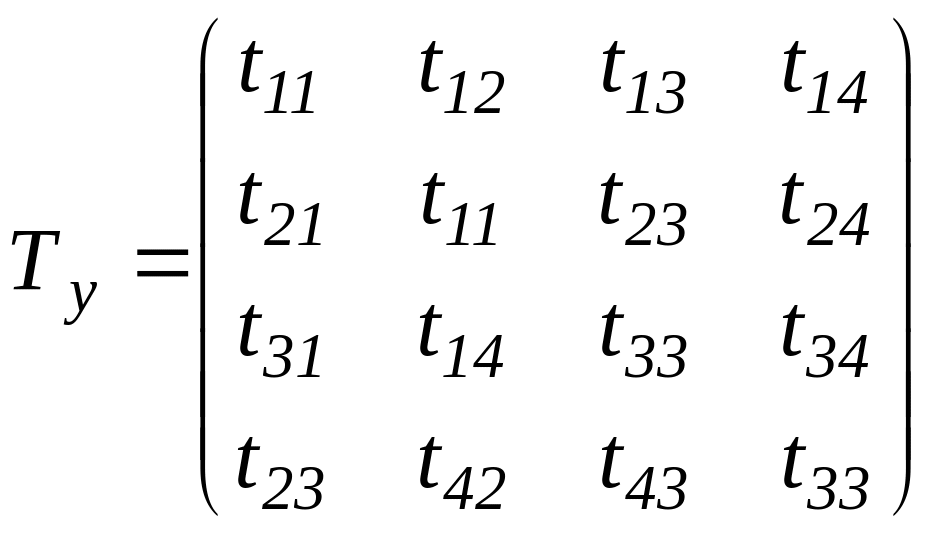(5.1.10)
Структуры матрицы коэффициентов В и структуру матрицы , которые в случае распространения в плоскости (хz) пьезоупругой волны в среде ромбической сингонии класса 222 имеют вид (3.1.11) и (4.2.10).
Элементы можно записать как
(5.1.11)
С учетом граничных условий для свободных и металлизированных границ слоя (5.1.4) уравнение (5.1.1) имеет вид:
Это уравнение приводит к алгебраической системе однородных уравнений
Условием существования нетривиальных решений является равенство нулю детерминанта:
(5.1.12)
Подстановка элементов tij из (5.1.11) в уравнение (5.1.12) дает уравнения дисперсии в пьезоэлектрических волн в явной аналитической форме:
(5.1.13)
Где
,
,
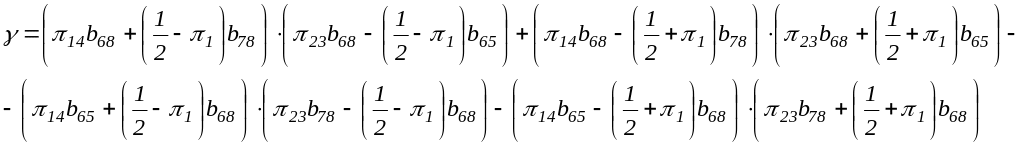
Уравнение дисперсии однородного слоя с жестко закрепленными и металлизированными границами следует из:
(5.1.14)
Где
,
,
.
Когда граница свободно – жестко закреплена и металлизирована, то уравнение дисперсии однородного слоя следует из
(5.1.15)
Где
,
,
,
.