3.2 Математичне моделювання пристрою перетворення кодів шляхом мінімізації визначених перемикальних функцій алгебри логіки за допомогою метода Квайна.

3.2.1 Мінімізація перемикальних функцій: основні поняття.

Процес спрощення перемикальної функції з метою отримання мінімальної нормальної форми називають мінімізацією.

Здійснюючи мінімізацію, виходять із вимоги мінімальної витрати обладнання, оскільки кожній елементарний логічній функції відповідає певний фізичний елемент.

Для мінімізації перемикальних фунцій застосовують різні методи: послідовного виключення змінних за допомогою законів і тотожностей алгебри логіки, Діаграм Вейча, мінімізованих карт Карно тощо.

Відзначимо, що досконала диз’юнктивна нормальна форма (ДДНФ) подання перемикальної функції являє собою запис даної функції у вигляді диз’юнкції констітуент 1 (мінтермів) - таких елементарних кон’юнкцій, для яких значення функції дорівнює одиниці.

Кожна констітуента 1 ДДНФ містить кожну змінну тільки один раз у прямому або інверсному вигляді для заданого набору значень змінних.

Алгоритм переходу від табличного задавання перемикальної функції до її запису в ДДНФ містить наведені нижче кроки.

Крок 1. Скласти мінтерми (констітуенти 1) для тих рядків таблиці істинності, на яких перемикальна функція дорівнює одиниці (якщо значення деякої змінної в рядку таблиці дорівнює нулю, то в мінтермі (констітуенті 1) записується заперечення цієї змінної).

Крок 2. Записати диз’юнкцію складених мінтермів (констітуент 1), що і буде являти собою перемикальну функцію в ДДНФ.

Дане правило називають правилом запису перемикальної функції по одиницях.

Наприклад, запис перемикальної функції, поданої в табл. 2.1, у ДДНФ буде мати наступний вигляд:

(2.1)

Таблиця 5 – Табличне подання логічної перемикальної функції

Номер набору	A	B	C	Y = f (A,B,C)
0	0	0	0	1
1	0	0	1	1
2	0	1	0	1
3	0	1	1	0
4	1	0	0	0
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

Попереднє подання перемикальної функції в формі ДДНФ дозволяє уникнути отримання в якості результату мінімізації даної функції тупикової форми (такої форми, що більше не спрощується, але не є мінімальною).

Розкриємо сутність методу Квайна на деяких прикладах перемикальних функцій

3.2.2 Метод Квайна. В процесі мінімізації БФ дуже часто використовується операція склеювання: AxA =A (її легко довести, дійсно, AxA =A (x )=A*1=A) 

Якщо до виразів Ax і A була застосована операція склеювання, то говорять, що вирази Ax і A склеюються по змінній x.

Метод Квайна знаходження скороченої днф базується на операції неповного склеювання: AxA =AAxA

Метод Квайна визначається наступним алгоритмом.

БФ f(x₁…x_n), що мінімізується, записується у вигляді ДДНФ. Починаючи з дднф (позначимо її f₀) будується послідовність днф f₀, f₁, f₂, ..., f_і до тих пір, доки дві ДНФ f_к та f_к+1 не співпадуть між собою. При цьому перехід від форми f_і до форми f_і+1 (і= ) відбувається згідно з наступним правилом: в формі f_і виконуються всі можливі операції неповного склеювання, які застосовуються до елементарних кон’юнкцій довжини n-i, де n – кількість змінних, від яких залежить дана БФ, а і – крок, на якому виконується операція неповного склеювання; далі виконуються всі можливі операції поглинання. Результатом застосування алгоритму Квайна є скорочена ДНФ.

Легко бачити, що застосувавши алгоритм Квайна, ми отримаємо скорочену ДНФ не пізніше, ніж за n кроків.

Приклад. Продемонструємо роботу алгоритму Квайна на прикладі БФ f, що задана своєю ДДНФ: .

Операцію неповного склеювання можна застосувати до першої і другої, першої і третьої, а також до першої і четвертої констітуент 1. В результаті ми отримаємо:

Після чотирикратного застосування операції поглинання форма перетворюється в форму

Оскільки операція неповного склеювання далі застосована бути не може, то форма співпадає з формою і, в силу метода Квайна, форма - скорочена ДНФ БФ . Вона містить в собі чотири простих імпліканти. Для подальшої мінімізації БФ необхідно побудувати ІТ, знайти ядро і т.д. 2.3 Розробка математичної моделі пристрою перетворення кодів згідно заданого варіанту вимог до вхідного потоку даних і методу мінімізації

Будемо виконувати мінімізацію визначених в завданні на дипломне проектування логічних перемикальних функцій та вимоги до вхідного потоку даних, застосовуючи до цих функцій метод діаграм Вейча (табл. 1.1).

Етап 1. Побудуємо табличне подання логічних перемикальних функцій відповідно до табл. 1.4 вхідних даних, представивши отриманий результат в табл. 2.2.

Таблиця 6 – Таблиця істинності (табличне подання перемикальних функцій алгебри логіки F₁-F₃)

В8	В7	В6	В5	В4	В3	В2	В1	F3	F2	F1	ПК
1	1	0	0	1	0	1	0	1	0	0	1
1	1	0	1	1	0	1	0	1	0	0	1
1	0	0	1	0	0	1	1	1	0	1	2
1	0	1	1	0	0	1	1	1	0	1	2
0	1	0	0	0	1	0	0	1	1	0	3
0	1	0	0	1	1	0	0	1	1	0	3
0	0	1	1	0	1	0	0	1	1	1	4
0	0	1	1	0	1	0	1	1	1	1	4
0	0	1	1	0	1	1	0	1	1	1	4
0	0	1	1	0	1	1	1	1	1	1	4
0	0	1	1	1	1	0	0	1	1	1	4
0	0	1	1	1	1	0	1	1	1	1	4
0	0	1	1	1	1	1	0	1	1	1	4
0	0	1	1	1	1	1	1	1	1	1	4
1	0	1	1	0	1	0	0	1	1	1	4
1	0	1	1	0	1	0	1	1	1	1	4
1	0	1	1	0	1	1	0	1	1	1	4
1	0	1	1	0	1	1	1	1	1	1	4
1	0	1	1	1	1	0	0	1	1	1	4
1	0	1	1	1	1	0	1	1	1	1	4
1	0	1	1	1	1	1	0	1	1	1	4
1	0	1	1	1	1	1	1	1	1	1	4

Етап 2. Знайдемо подання початкових перемикальних функцій F₁-F₃ у ДДНФ (досконалій диз’юнктивній нормальній формі), представивши його за допомогою формул (2.3) – (2.5).

F₃=                      .

(2.3)

F₂=                  . (2.4)

F₁=                   . (2.5)

Етап 3. З метою скорочення процедури застосування алгоритму Квайна позначимо констітуенти 1 із ДДНФ функції F₃ наступними десятковими числами, взятими в квадратні дужки:

F₃=      [6]   [8]     [12]       [18]   [20]   .

Етап 4. Застосуємо операцію неповного склеювання (2.1) до елементарних кон’юнкцій отриманого виразу (n=8, i=0), враховуючи ознаку належності до комп’ютера:

[1]  [2] = [1]  [2] 

[3]  [4] = [3]  [4] 

[5]  [6] = [5]  [6] 

[7]  [8] = [7]  [8] 

[9]  [10] = [9]  [10] 

[11]  [12] = [11]  [12]  

[13]  [14] = [13]  [14]  

[15]  [16] = [15]  [16] 

[17]  [18] = [17]  [18]  B₂ (11)

[19]  [20] = [19]  [20] 

[21]  [22] = [21]  [22]  (2.1)

Етап 5. Виконавши операцію поглинання (2.2), отримаємо наступне представлення функції F₃ після першого кроку застосування алгоритму Квайна. Знову позначимо елементарнї кон’юнкції із ДНФ функції F’₃ наступними десятковими числами, взятими в квадратні дужки:

F’₃ =         B₂ (11)[9]   [11].

Етап 6. Застосуємо операцію неповного склеювання (2.1) до елементарних кон’юнкцій ДНФ функції F’₃ (n=8, i=1), враховуючи ознаку належності до комп’ютера:

[4]  [5] = [4]  [5] 

[6]  [7] = [6]  [7]  

[8]  [9] = [8]  [9] 

[10]  [11] = [10]  [11] 

Етап 7. Виконавши операцію поглинання (2.2), отримаємо наступне представлення функції F₃ після другого кроку застосування алгоритму Квайна (з позначенням елементарних кон’юнкцій із ДНФ функції F’’₃ десятковими числами, взятими в квадратні дужки):

F’’₃ =      .

Етап 8. Застосуємо операцію неповного склеювання (2.1) до елементарних кон’юнкцій ДНФ функції F’’₃ (n=8, i=2), враховуючи ознаку належності до комп’ютера:

[4]  [5] = [4]  [5]   (11)

[6]  [7] = [6]  [7]  (11)

Етап 9. Виконавши операцію поглинання (2.2), отримаємо наступне представлення функції F₃ після третього кроку застосування алгоритму Квайна (з позначенням елементарних кон’юнкцій із ДНФ функції F’’₃ десятковими числами, взятими в квадратні дужки):

F’’’₃ =     (11)[4]  (11)[5].

Етап 10. Застосуємо операцію неповного склеювання (2.1) до елементарних кон’юнкцій ДНФ функції F’’’₃ (n=8, i=3), враховуючи ознаку належності до комп’ютера:

[4]  [5] = [4]  [5]  (11)

Етап 11. Виконавши операцію поглинання (2.2), отримаємо наступне представлення функції F₃ після третього кроку застосування алгоритму Квайна (з позначенням елементарних кон’юнкцій із ДНФ функції F’’₃ десятковими числами, взятими в квадратні дужки):

F’’’’₃ =    (11)[4].

(2.6)

Оскільки операція неповного склеювання (2.1) до елементарних кон’юнкцій ДНФ функції F’’’’₃ застосована бути не може, то вираз (2.6):

F’’’’₃ =    (11) - скорочена ДНФ функції F₃.

Скорочені ДНФ функцій F₁ і F₂ можна знайти із скороченої ДНФ функції F₃. Легко бачити, що:

скорочена ДНФ функції F₂ =  (11),

(2.7)

а скорочена ДНФ функції F₁ =  (11)

(2.8).

3.2.3 Знаходження тупикових і мінімальних ДНФ функцій F₃ , F₂ і F₁. Легко бачити, що прості імпліканти, які входять у скорочені ДНФ функцій F₃ , F₂ і F₁, утворюють ядра цих функцій, тому функції F₃ , F₂ і F₁ будуть мати по одній тупиковій ДНФ, яка буде співпадати з МДНФ відповідної функції. Тому побудова імплікантних таблиць для функцій F₃ , F₂ і F₁ не потрібна і тому

МДНФ F₃ =    (11) (2.9)

МДНФ F₂ =  (11) (2.10)

МДНФ F₁ =  (11) (2.11).

Використовуючи методи сумісної мінімації систем БФ систему функцій, функції F₃ , F₂ і F₁ можна записати з ознаками належності простих імплікант до тієї чи іншої функції (як ми побачимо в наступному підрозділі, використання методів сумісної мінімації систем БФ дозволяє суттєво скоротити затрати обладнання в керуючому пристрої). В результаті отримаємо:

F₃ =    (3,2,1) (2.12)

F₂ =  (3,2,1)

(2.13)

F₁ =  (3,2,1)

(2.14).

Вирази (2.12), (2.13), (2.14) являються остаточною математичною моделлю керуючого пристрою.

Рисунок 3 – Структурна схема для перетворювача керуючого коду

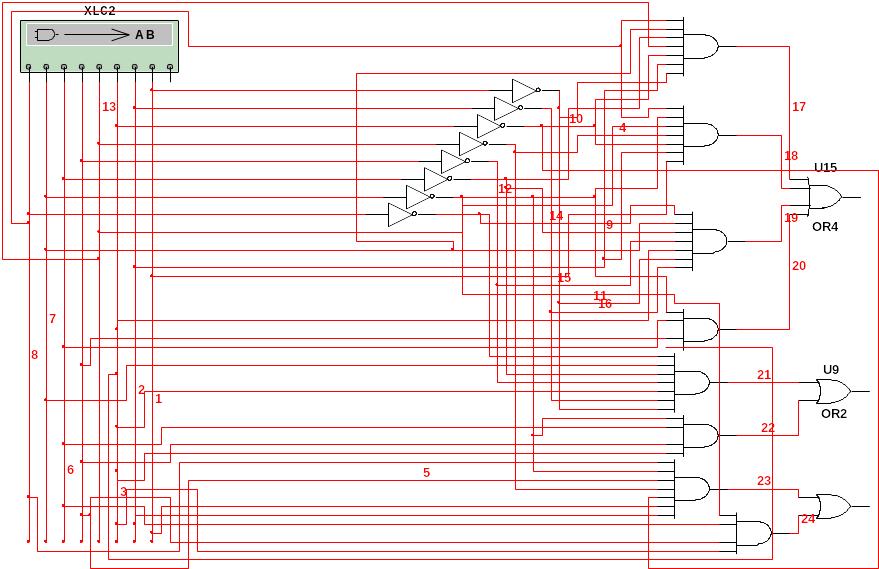
Отримані в середовищі Multisim таблиці істинності моделей (2.6)-(2.8) функціонування керуючого пристрою у вигляді перемикальних функцій F₃-F₁ підтвердила працездатність цього пристрою.

Додаток А

	1		2	3		4	5		6	7	8		9	10			11		12		13		14		15		16		17		18		19		20		21
1													˅
2	˅
3	˅
4	˅
5				˅
6				˅
7				˅
8				˅
9
10													˅																˅
11														˅
12														˅
13																			˅
14																			˅
15																			˅
16																			˅
17																																					˅
18																													˅
19																															˅
20																															˅
21
А		В			С			D				H
1		0
1		1			0
1		1			0
1		1			0
1		1			1			0
1		1			1			0
1		1			1			0
1		1			1			0
0
2		1			0
1		1			1			0
1		1			1			0
1		1			1			1				0
1		1			1			1				0
1		1			1			1				0
1		1			1			1				0
1		0
1		1			0
1		1			1			0
1		1			1			0
0

Зміст: