Оцінка точності

Середня квадратична похибка одиниці ваги

Ваги віддалей

Похибки віддалей

Похибка в положенні ШСЗ

Робота №3. Зрівноваження супутникової тріангуляції Вступні відомості

Виміряними величинами у супутникових мережах можуть бути: а) напрямки на ШСЗ, отримані від обробки фотографічних спостережень; б) віддалі до ШСЗ, отримані лазерними або радіо-віддалемірами; в) віддалі та напрямки. У відповідності з цим розглядають три види космічних геодезичних мереж:

1. Супутникова тріангуляція.

2. Супутникова трилатерація.

3. Супутникова векторна мережа (хорда).

Площиною синхронізації називають площину, яка проходить через два пункти спостережень і ШСЗ в момент синхронних спостережень.

Топоцентричним радіусом-вектором називають вектор, з’єднуючий пункт спостереження і ШСЗ.

Замикаючим напрямком називають напрямок хорди, яка з’єднує два пункти спостережень ШСЗ. Він характеризується трьома направляючими косинусами M₁₂, N₁₂, R₁₂ (косинусами кутів між хордою і осями координат) або двома сферичними кутами ₁₂, ₁₂ (з площиною екватора і гринвіцького меридіана).

Ідея супутникової тріангуляції полягає в тому що по синхронним фотографічним спостереженням ШСЗ з двох пунктів можна визначити напрямок хорди Р₁Р₂ (але не її довжину). Такі спостереження складають умову компланарності трьох векторів у вигляді визначника

А звідси отримають рівняння площини синхронізації

або

Спостереження другого ШСЗ (або повторне спостереження першого) дає рівняння другої площини синхронізації (див мал. 6)

Із сумісного рішення цих двох рівнянь можна отримати рівняння прямої, по якій вони перетинаються, тобто хорди Р₁Р₂ Р₃ (довжини яких можуть досягати декількох тисяч кілометрів), то можна визначити кути цього „хордового” трикутника (див мал. 7)використовуються формули виду

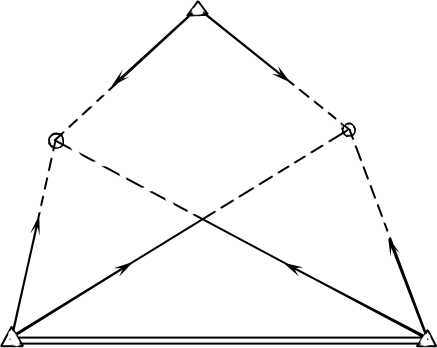
Очевидно, ₁+₂+₃ =180^ (а не 180^+Е, тому що ми маємо справу з плоским трикутником)

Застосовують наступні побудови супутникової тріангуляції:

1. Пряма просторова засічка (мал. 5). В ній є два вихідні пункти і один ШСЗ, що визначається

Виміряних величин – 4

Невідомих – 3

Надлишкових вимірів – 1 .

2. Обернена просторова засічка (мал. 8). У цій побудові два вихідних пункти, два ШСЗ і один пункт, що підлягає визначенню

Вимірів – 12

Невідомих – 9

Надлишкових вимірів – 3 .

3. Засічка пункту, замикаючими напрямками (мал. 9). Маємо два вихідних пункти, чотири ШСЗ і один пункт, що підлягає визначенню

Вимірів – 16

Невідомих – 15

Надлишкових вимірів – 1 .

4. Засічка пункту площинами синхронізації (мал. 10). В ній два вихідні пункти три ШСЗ і один пункт, що підлягає визначенню

Вимірів – 16

Невідомих – 15

Надлишкових вимірів – 1 .

В окремих випадках виміряними величинами вважають сферичні кути хорд _ік, _ік, отримані із обробки синхронних фотографічних спостережень.

Супутникова тріангуляція має ряд особливостей, так як напрямки між її пунктами визначають незалежно один від одного в одній зоряній системі координат. Тому в ній не можуть виникати кутові умови (сум і азимутів). Полюсні, базисні і координатні умови зберігаються, але мають дуже складний вигляд. Крім того, в ній виникають особливі умови:

1. Компланарність трьох векторів , які у випадку синхронних спостережень повинні лежати в одній площині.

2. Пучка площин (всі площини синхронізації для двох пунктів спостережень повинні перетинатися по одній хорді р₁, р₂).

3. Зв’язки площин. Перетин трьох площин синхронізації дає одну точку. Наявність четвертої площини веде до умови перетину всіх чотирьох площин в одній точці.

Для зрівноваження супутникових мереж тріангуляції застосовують три методи:

1. Параметричний, в якому зрівноваження похибок виміряних величин ’ і ’ (обернених гринвіцьких часових кутів та схилень) рішають за умови:

Рівняння похибок в даному випадку прості і стандартні (що зручно для обчислень на ЕОМ), але необхідно визначити наближені координати пунктів і ШСЗ X^, Y^, Z^

2. Корелатний метод з додатковими невідомими (метод умовних вимірів). При цьому умовні рівняння площин синхронізації рішаються за умови

де К_і – корелати, а , ,  - додадкові невідомі (поправки в напрямки і довжини хорд або в координати пунктів).

Лише ці два способи є цілком строгими, якщо в мережі маємо спостереження ШСЗ більш ніж з двох пунктів.

3. Метод замикаючих напрямків. У цьому методі спочатку рішають рівняння похибок для кожної замикаючої під умовою і отримають сферичні кути „замикаючих” _ік, _ік. Після вважають виміряними величинами і рішають рівняння похибок цих кутів під умовою

Метод являється строгим для мережі побудованій по методу замикаючих напрямків.

Найбільший порядок мають матриці в параметричному та корелатному методах, але для ЕОМ перший зручніший.

Нижче буде розглянутий параметричний метод зрівноваження супутникової тріангуляції. У цьому випадку виміряними величинами являються ’ і ’, які є функціями невідомих параметрів – прямокутних координат X, Y, Z ШСЗ і визначаємих пунктів. Для двох пунктів І і К рівняння поправок

де вільні члени l находяться як різниці „обчислені значення мінус виміряні”

При цьому

де X^, Y^, Z^ - наближені координати ШСЗ і визначаємих пунктів, які можуть бути отримані із рішення прямих просторових засічок (див. Роботу №2).

Коефіцієнти а, в, с представляють собою частинні похідні виду

Число рівнянь поправок дорівнює числу вимірів, тобто подвоєному числу напрямків на ШСЗ, які спостерігались; число нормальних рівнянь – числу невідомих координат, тобто потроєному числу ШСЗ і визначаємих наземних пунктів.

Отримавши наближені координати ШСЗ і пунктів, спочатку складають рівняння поправок і обчислюють їх вільні члени і коефіцієнти. Після складають і рішають нормальні рівняння, із рішення яких находять поправки наближених координат X, Y, Z.

Для контролю два рази находять зрівноважені значення виміряних величин: 1) як виміряні значення поправок мінус поправки V , 2) як обчисленні по зрівноваженим координатам.

Для оцінки точності обчислюють:

1. середню квадратичну похибку одиниці ваги

2. ваги координат самого слабого пункту Р_n по способу Енке.

Так, для прямої просторової засічки:

3. похибки координат і положення пункту Р