2.5 Расчёт поперечной арматуры ригеля

Максимальные поперечные силы, действующие в приопорных частях

балки, найдем из условия равновесия балки (рис.2.4).

_{Рисунок 2.4 -} Расчетная схема к определению опорных реакций в ригеле

.

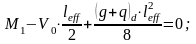
Рисунок 2.5 – Расчётная схема к определению опорных реакций в ригеле

Максимальная поперечная сила возникает на первой опоре.

.

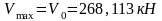Расчет прочности железобетонных элементов на действие поперечных сил начинается проверкой условия:

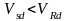
где

V_sd - расчетная поперечная сила от внешних воздействий;

V_Rd -сила, воспринимаемая железобетонным элементом без поперечного армирования.

но не менее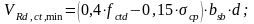

где

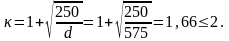Принимаем κ=1,66

;

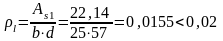σ_ср= 0 - при отсутствии осевого усилия (сжимающей силы)

где

Так как условие не выполняется, то для обеспечения прочности элементов по наклонному сечению, поперечную арматуру необходимо устанавливать по расчету.

Расчетное сечение назначаем на расстоянии от опоры

z=h-2·c = 600-2·30=540 мм.

Рисунок 2.6– Расчётное сечение

_{Рисунок 2.7– Расчётная схема}

.

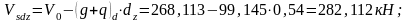
На всех приопорных участках, равных l/4 пролета, принимаем шаг поперечных стержней 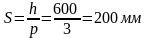. (табл. П13[1])

В средней части пролёта .

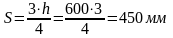Определяем продольные относительные деформации в растянутой арматуре, предварительно задавшись углом наклона трещин к горизонтали 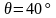, по формуле:

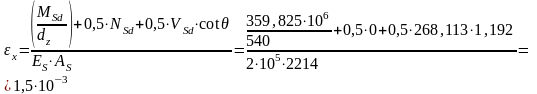
Для того, чтобы выяснить верно ли был задан угол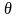 необходимо воспользоваться таблицей 7.1[4]. Предварительно определим касательные напряжения, действующие в рассматриваемом сечении:

;

Тогда

.

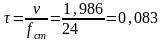В соответствии со значениям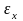и и 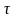по таблице 7.1[4] определяем правильность принятия значения угла . В нашем случаи угол наклона трещин к горизонтали получился 39, 36⁰.

Определяем средние значения главных растягивающих деформаций 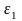(значение определяется итерационным путём):

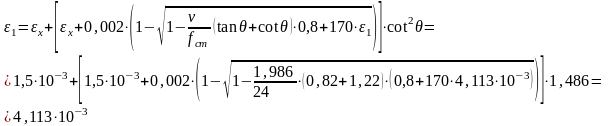
Несущая способность наклонного сечения определяется:

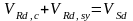
где

- составляющая поперечной силы воспринимаемая бетоном, кН;

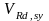- составляющая поперечной силы воспринимаемая поперечной арматурой,кН.

Определяем составляющую поперечной силы , воспринимаемой бетоном:

,

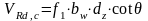где:

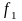- главные растягивающие напряжения, МПа

Главные растягивающие напряжения определяем по формуле:

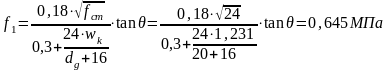
где

- максимальный размер заполнителя; =20мм;

- ширина раскрытия наклонной трещины.

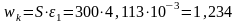
где S = 300 мм – расстояние между диагональными трещинами.

Составляющая поперечной силы, воспринимаемая бетоном будет равна:

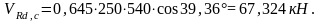
Составляющая поперечной силы, которую должна воспринять арматура, равна:

Составляющая поперечной силы, воспринимаемая арматурой, определяется по формуле:

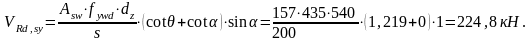
где

α – угол наклона поперечной арматуры к продольной оси элемента, α=90°.

Количество поперечной арматуры рассчитываем, приняв условие, что напряжение в ней достигают предела текучести: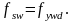

Предварительно задавшись шагом поперечной арматуры определяем её площадь.

Принимаем шаг поперечной арматуры S=200 мм. Согласно таблице 7.5[4] минимальный коэффициент поперченного армирования для заданного класса бетона и класса арматуры 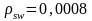. Тогда площадь поперечного сечения арматуры при шаге S=200 мм должна быть не менее:

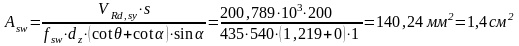
Принимаем 2 Ø 10, A_sw=1,57 см²

Действительная несущая способность наклонного сечения составляет:

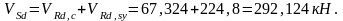
V_Sd должно удовлетворять условию:

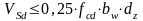
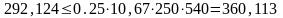кН

Условие выполняется, следовательно расчет поперечной арматуры ригеля выполнен верно