Резонанс напряжений

Если в цепи переменного тока, содержащей последовательно включенные конденсатор, катушку индуктивности

, (1)

то угол сдвига фаз между током и напряжением обращается в нуль ( = 0), т. е. изменения тока и напряжения происходят синфазно. Условию (1) удовлетворяет частота

. (2)

В данном случае полное сопротивление цепи Z становится минимальным, равным активному сопротивлению R цепи, и ток в цепи определяется этим сопротивле­нием, принимая максимальные значения. При этом падение напряжения на активном сопротивлении равно внешнему напряжению, прило­женному к цепи (U_R = U), а падения напряжений на конденсаторе (Uс) и катушке индуктивности (U_L) одинаковы по амплитуде и противоположны по фазе. Это явление называется резонансом напряжений (последовательным резонансом), а частота (2) - резонансной частотой. Векторная диаграмма для резонанса напряжений при­ведена на рис. 11.8, а зависимость амплитуды силы тока от  уже была дана на рис. 11.5. Явление резонанса напряжений используется в технике для усиления колебаний напряжения какой-либо определенной частоты.

LI₀

₀

RI₀

Рис. 11.8.

Резонанс токов

Рассмотрим цепь переменного тока, содержащую параллельно включенные конден­сатор емкостью С и катушку индуктивностью L (рис. 11.9). Для простоты допустим, что активное сопротивление обеих ветвей настолько мало, что им можно пренебречь. Если разность потенциалов клемм идеального источника гармонической ЭДС равна

,

то в ветви 1С2 течет ток

.

Аналогично, сила тока в ветви 1L2

.

Рис. 11.9.

Разность фаз токов в ветвях равна , то есть токи в ветвях противоположны по фазе. Амплитуда силы тока во внешней неразветвленной цепи

.

Если , то . Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при приближении частоты приложенной ЭДС к резонансной частоте называется резонансом токов (параллельным резонансом). Свойства резонанса токов используют в резонансных усилителях, позволяющих выделять одно определенное колебание из сигнала сложной формы. Резонанс токов используется в индукционных печах, где нагревание металлов производится вихревыми токами.

Мощность, выделяемая в цепи переменного тока

Действующим или эффективным значением периодического тока называется среднее квадратичное значение силы тока за период Т его изменения:

.

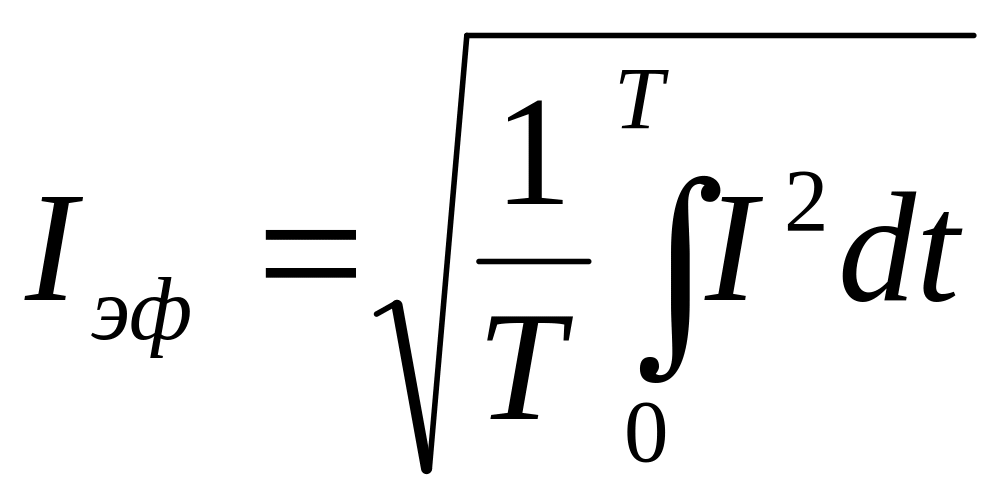Для синусоидального тока и синусоидальной ЭДС действующие значения равны

,

.

Элементарная работа, совершаемая синусоидальным током за малое время dt равна работе источника ЭДС за то же время:

.

Мгновенная мощность тока в цепи

.

Среднее за период значение мгновенной мощности называется активной мощностью Р тока в электрической цепи:

.

Множитель cos называется коэффициентом мощности. Так как , cos = R/Z, то

.

При резонансе Z имеет минимальное значение, равное R, и активная мощность тока максимальна:

.

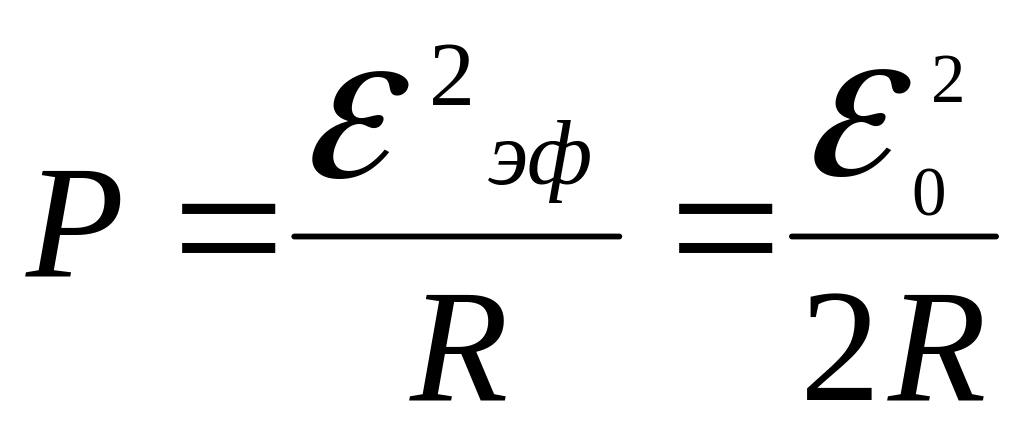Если вынуждающая ЭДС представляет собой сумму гармонических ЭДС с различными циклическими частотами _i, то результирующий электрический ток в колебательном контуре также будет представлять сумму синусоидальных токов с циклическими частотами _i. Однако вследствие явления электрического резонанса контур сильнее всего реагирует на ту составляющую ЭДС, частота _i которой равна или наиболее близка к резонансной частоте ₀ контура. Поэтому сила тока в контуре в основном определяется этой составляющей ЭДС.

Влияние на колебательный контур вынуждающих ЭДС, частоты которых отличны от ₀, будет тем слабее, чем острее резонансная кривая для контура, т.е. чем резче зависимость I₀ от  вблизи значения  = ₀. Остроту резонансной кривой можно охарактеризовать с помощью относительной ширины этой кривой, равной  = ₀, где  - разность значений  ₂ и ₁ частот, соответствующих I₀ = I_0макс/ (рис. 11.10).

Рис. 11.10.

Относительная ширина резонансной кривой колебательного контура равна отношению активного сопротивления контура к его волновому сопротивлению:

.

Относительная ширина резонансной кривой колебательного контура есть величина, обратная добротности контура:

.