Вынужденные колебания
Для осуществления вынужденных колебаний в электрическом колебательном контуре в него нужно включить источник электрической энергии, ЭДС которого изменяется с течением времени (рис. 11.4).
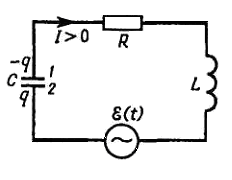
Рис.11.4.
Уравнение вынужденных электрических колебаний в контуре
.
( )
Здесь
=R/(2L)
- коэффициент затухания свободных
колебаний в контуре, а 0=
- циклическая частота свободных
незатухающих колебаний (т. е. при R
= 0).
Если
вынуждающая ЭДС изменяется по
гармоническому закону:
,
то при установившихся вынужденных
колебаниях заряд конденсатора колеблется
гармонически с той же циклической
частотой :
.
(.)
Амплитуда А и начальная фаза 0 находятся по формулам:
,
.
Учитывая, что
и
,
получим
,
.
Найдем силу тока при установившихся вынужденных колебаниях в контуре:
(.)
Амплитуду тока I0=
и начальную фазу -
=о+/2
определим как:
,
.
Резонанс
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей переменной ЭДС к собственной частоте колебательной системы называется резонансом.
Графики зависимости I0() при различных R называются резонансными кривыми колебательного контура (рис. 11.5). Графики зависимости () показаны на рис. 11.6. Резонансная циклическая частота р, соответствующая максимуму амплитуды тока в контуре при вынужденных колебаниях, не зависит от R:
р = 0 = . (.)
Амплитуда силы тока при резонансе I0(Р)= 0/R, а сдвиг фаз между силой тока и ЭДС (р) = 0.
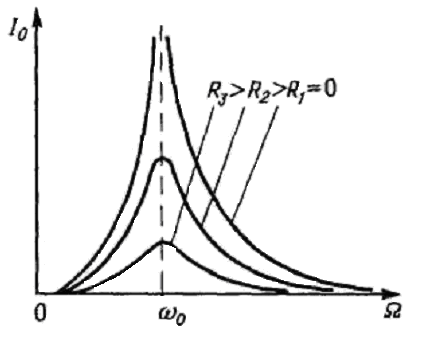
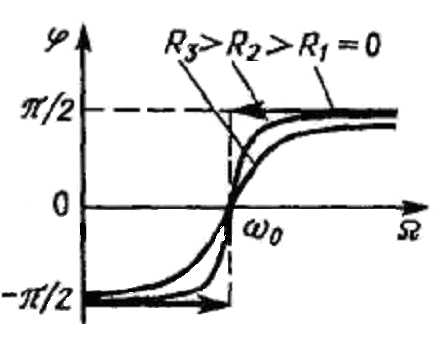
Рис.11.5. Рис.11.6.
Установившиеся вынужденные электромагнитные колебания можно рассматривать как протекание в цепи, содержащей резистор, катушку индуктивности и конденсатор, переменного тока.
Рассмотрим цепь переменного тока, содержащую последовательно включенные резистор, катушку и конденсатор
Разность потенциалов клемм идеального источника гармонической ЭДС равна его ЭДС
.
( . )
Падение потенциала на отдельных участках показанной на рис. 11.4 цепи переменного синусоидального тока I = I0cos(t - ) - конденсаторе емкостью С, резисторе сопротивлением R и катушке индуктивностью L
,
,
.
Колебания uR происходят в одной фазе с колебаниями тока в цепи; uL опережает ток по фазе на /2, а ис отстает от него по фазе на /2, причем, по закону Ома для участка цепи
.
Фазовые соотношения можно представить с помощью векторной диаграммы (рис. 11.7).
UL
U
URR
UC
Рис. 11.7.
Амплитудные значения UC , UR и Ul соответственно равны:
,
,
или
,
,
,
где Xc=1/(C) - емкостное сопротивление, ХL= L- индуктивное сопротивление, a R - активное электрическое сопротивление. Величины
,
называются соответственно реактивным и полным сопротивлениями цепи.