14

Лекция Электромагнитные колебания Свободные незатухающие колебания

Для возбуждения электромагнитных колебаний служат систе­мы, называемые колебательным контуром (рис. 11.1), состоящие из параллельно соединенных между собой индуктивности L и ем­кости С. Рассмотрим идеальный контур, т. е. контур, омическое сопротивление которого равно нулю (R = 0).

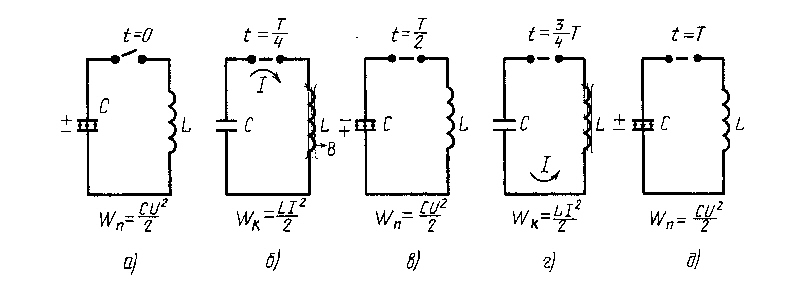
Рис. 11.1.

Чтобы возбудить колебания в этом контуре, необходимо либо сообщить обклад­кам конденсатора некоторый заряд, либо возбудить в катушке индуктивности ток. Пусть в начальный момент времени конден­сатор заряжен до разности потенциалов U_o (рис. 11.1, а); следова­тельно, он обладает потенциальной энергией

.

В этот момент времени ток в катушке I = 0. В идеальном контуре через четверть периода вся энергия электрического поля переходит в энергию магнитного поля W_m = LI₀²/2 (рис. 11.1, б). В этом случае напряжение между обкладками конденсатора равно нулю: U = 0, а через катушку протекает максимальный ток I₀ (рис. 11.1, б).

Если линейные размеры контура l не слишком велики (l << c/, где с – скорость света в вакууме,  - частота колебаний в контуре), то можно считать, что в каждый момент времени сила тока во всех частях контура одинакова. Такой переменный ток называется квазистационарным.

Свободные электромагнитные колебания в колебательном контуре являются гармоническими, если его электрическое сопротивление R = 0:

. (11.1)

Формула (11.1) является дифференци­альным уравнением гармонического колебания; его решением будет

q = q₀sin(t+_о). (11.2)

Согласно принятым обозначениям,

(11.3)

откуда T=2/ .

Выражение (11.3) называется формулой Томсона и показывает, что при R = 0 период электромагнитных колебаний, возникающих в контуре, определяется только значениями индуктивности L и емкости С.

По гармоническому закону изменяется не только заряд на обкладках конденсатора, но и напряжение и сила тока в контуре:

. (11.4)

. (11.5)

Из выражений (11.2), (11.4), (11.5) вытекает, что колебания заряда (напряжения) и тока в контуре сдвинуты по фазе на /2.

Волновое сопротивление контура определяется выражением .

Превращение энергии в колебательном контуре

При зарядке конденсатора между его обкладками появляется электрическое поле, энергия которого

.

При разрядке конденсатора на катушку индуктивности в ней возникает магнитное поле, энергия которого

.

Значения W_e и W_m изменяются при гармонических электромагнитных колебаниях от 0 до максимальных значений. Причем колебания W_e и W_m сдвинуты по фазе. Если W_e = 0, то W_m = (W_m)_max = . Если W_m = 0, то W_e = (W_e)_max = . Полная энергия электромагнитных колебаний в колебательном контуре не изменяется с течением времени:

.