2.1.Линейная регрессия и корреляция: смысл и оценка параметров.

Линейная регрессия находит широкое применение в эконометрике в виде четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида:

y=a+bx+E или y^Т_x=a+bx – позволяет по заданным фактическим значениям фактора x иметь теоретические значения результативного признака.

На графике теоретические значения представляют линию регрессии (см. рис.):

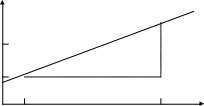
Построение линейной регрессии сводится к оценке ее параметров — а и b. Оценки параметров линейной регрессии могут быть найдены разными методами:

1.) можно обратиться к полю корреляции и, выбрав на графике две точки, провести через них прямую линию (см. рис.). Далее по графику можно определить значения параметров. Параметр а определим как точку пересечения линии регрессии с осью оу, а параметр b оценим, исходя из угла наклона линии регрессии, как b=tg=dy/dx , где dy — приращение результата y, а dx — приращение фактора х.

2.) Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

МНК позволяет получить такие оценки параметров а и b при которых сумма квадратов отклонений фактических значений результативного признака у от расчетных (теоретических) y^Т_x минимальна:

. Т.к. , то

Т.е., из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной.

Чтобы найти минимум функции надо вычислить частные производные по каждому из параметров a и b и прировнять их к нулю:

Преобразуя формулы, получим следующую систему нормальных уравнений для оценки параметров а и b:

Решая систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров а и b. Можно воспользоваться следующими готовыми формулами:

(эта формула получена путём деления первого уравнения системы на n).

, где - ковариация признаков;

- дисперсия признака x.

.

Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.

Формально а — значение у при х = 0. Если признак-фактор х не имеет и не может иметь нулевого значения, то вышеуказанная трактовка свободного члена а не имеет смысла. параметр а может не иметь экономического содержания. Попытки экономически интерпретировать параметр а могут привести к абсурду, особенно при а < 0.

Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора.,т.е. вариация результата меньше вариации фактора - коэффициент вариации по фактору х выше коэффициента вариации для результата у: V_x >V_y.

Где - коэффициент вариации по x;

- среднеквадратическое отклонение x;

- среднеарифметическое отклонение x.

Если переменные х и у выразить через отклонения от средних уровней, то линия регрессии на графике пройдет через начало координат: y^’т=bx^’

где и .

Оценка коэффициента регрессии при этом не изменится.

Оценку коэффициента регрессии можно получить проще, не обращаясь к методу наименьших квадратов. Альтернативную оценку параметра b можно найти исходя из содержания данного коэффициента: изменение результата сопоставляют с изменением фактора .

Эта величина является приближенной, ибо большая часть информации, имеющейся в данных, не используется при ее расчете. Она основана только на минимальных и максимальных значениях переменных.

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции r_xy.. Некоторые формулы линейного коэффициента корреляции:

Линейный коэффициент корреляции находится в границах: -1≤r_xy≤1.

Если коэффициент регрессии b>0, то 0≤r_xy≤1, при b<0, -1≤r_xy≤0.

Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствие связи между признаками. При иной спецификации модели связь между признаками может оказаться достаточно тесной.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции r_xy², называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:

.

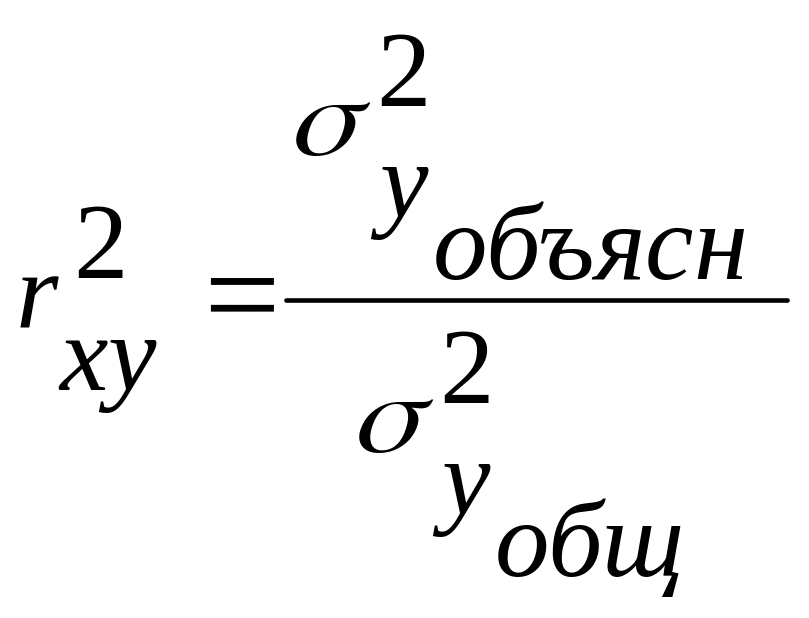Величина коэффициента детерминации служит одним из критериев оценки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов, и, следовательно, линейная модель хорошо аппроксимирует исходные данные и ею можно воспользоваться для прогноза значений результативного признака. Соответственно величина 1-r² характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.