18. Условие прочности конструкции. Три основные задачи, решаемые с использованием этого условия.

Условие прочности

Ответы на вопросы о прочности может дать оценка прочности конструкции, которая сводится к сравнению расчетных напряжений с допускаемыми:

_max [ ], _max [ ].

Это и есть основные условия прочности.

Расчетное напряжение - наибольшее по абсолютной величине сжимающее или стягивающее напряжение, возникающее в опасном сечении конструкции.

Три основные задачи, решаемые с использованием этого условия.

Условие прочности позволяет решать три типа задач:

1. Проверка прочности (проверочный расчет)

2. Подбор сечения (проектировочный расчет)

3. Определение грузоподъемности (допускаемой нагрузки)

19. Чистый сдвиг. Закон Гука при сдвиге. Связь между упругими постоянными материала. Удельная потенциальная энергия деформации при сдвиге. Закон парности касательных напряжений.

Чистый сдвиг – такое напряженное состояние, когда на гранях выделенного элемента возникают только касательные напряжения τ.

Наиболее просто однородный чистый сдвиг может быть осуществлен непосредственный нагружением пластины, захваченной в жесткие контурные шарнирно соединенные накладки. Для всех точек пластины касательные напряжения τ будут следующими:

τ = , где - толщина пластины.

Определим величину и направление главных напряжений при чистом сдвиге:

так как σ_x=σ_y=0, то можем записать

Направление главных площадок определяется углом α, который найдем по формуле

учитывая, что σ_x=σ_y=0

Касательные напряжения, действующие по боковым граням рассматриваемого параллелепипеда, являются экстремальными, а эти грани являются площадками сдвига и образуют с главными площадками углы, равные 45°

Следовательно, при чистом сдвиге нормальные напряжения на любых двух взаимно перпендикулярных площадках равны друг другу по величине и противоположны по знаку. Поэтому чистым сдвигом можно называть такое плоское напряженное состояние, при котором нормальные напряжения на двух взаимно перпендикулярных площадках равны друг другу по величине и противоположны по знаку.

Закон Гука при сдвиге

Касательные напряжения пропорциональны углу сдвига в определенных пределах упругой деформации сдвига. Соотношение τ = Gγ - формула закона Гука при сдвиге.

Коэффициент пропорциональности G в формуле закона Гука при сдвиге - модуль сдвига. Модуль сдвига измеряется в МПа, кН/см2, кгс/см2, кгс/мм2. Угол сдвига –безразмерная величина.

Модуль сдвига (G) – это физическая постоянная для материала, характеризующая жесткость при сдвиге. Значение модуля сдвига (G) может быть определено экспериментально.

Связь между упругими постоянными материала

Они характеризуют способность материала сопротивляться различным видам деформаций при воздействии на них внешних нагрузок.

Модуль Юнга или модуль упругости первого рода E характеризует сопротивляемость материала деформированию в направлении воздействия растягивающих или сжимающих нагрузок. Модуль Юнга является коэффициентом пропорциональности между нормальным напряжением и относительной линейной деформацией в законе Гука, записанном в дифференциальной форме: . На основе этой формулы находят опытным путём значение модуля упругости

где

Коэффициент Пуассона характеризует способность материала сопротивляться поперечному деформированию, т.е. изменению размеров в направлении, перпендикулярном воздействию силы.

Модуль сдвига или модуль упругости второго рода G характеризует сопротивляемость материала угловым деформациям при воздействии пары сил. Он является коэффициентом пропорциональности между касательным напряжением и углом сдвига в законе Гука при сдвиге, записанном в дифференциальной форме: .

модуль сдвига определяют косвенным путём, исходя из теоретической зависимости между тремя упругими постоянными:

Удельная потенциальная энергия деформации при сдвиге.

Удельная потенциальная энергия деформации и равна сумме удельной потенциальной энергии изменения объема и удельной потенциальной энергии изменения формы.

-удельная потенциальная энергия при сдвиге и измеряется в Дж/м³

Закон парности касательных напряжений.

Элементарный параллелепипед должен находиться в равновесии (он не должен вращаться вокруг оси x, проходящей через точку К) (см. рис. 6.3), поэтому суммарный момент всех сил, возникающих по граням относительно этой оси должен быть равным нулю:

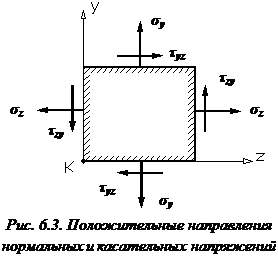
Формулировка закона парности касательных напряжений: касательные напряжения на любых двух взаимно перпендикулярных площадках, направленные по перпендикуляру к линии пересечения площадок, равны по величине, притом касательные напряжения либо сходятся к линии пересечения площадок, либо расходятся от нее.