6. Деформации и перемещения при растяжении-сжатии. Коэффициент Пуассона.

Определим абсолютное удлинение ∆L: N/A=E*∆L/L

∆L=NL/EA, если брус состоит из нескольких участков, то общее удлинение определяется путем суммирования по участкам. При решении большинства практических задач, возникает необходимость наряду с деформациями вызванными напряжением, учитывать также деформации вызванные изменением температуры, в этом случае пользуются методом наложения, т.е. силовая и температурная деформации, учитываются по отдельности.

∆Lобщ = ∆L+∆Lt = NL/EA+ αL∆t, α-коэф. расширения.

Коэффициент Пуассона.

При растяжении-сжатии, наряду с продольной деформацией возникает поперечная. Опытным путем установлена следующая зависимость ε_поп= -μ*ε_прод

μ- коэффициент Пуассона, постоянная для материала. Определяется экспериментально.

0<μ<0,5 – для всех материалов

0,25 < μ < 0,35 – для металлов, μ_ст = 0,3

7. Принципы разбиения бруса на участки. Температурное удлинение.

Для определения внутренних сил применяется метод сечения, суть которого заключается в след-м (РОЗУ):

• Рассматриваемое тело делится на две части

• Масленно отбрасывается одна из частей

• Действия отброшенной на оставшуюся заменяются внутренними силовыми факторами

• Из ур-я равновесия оств-ся части, определяют неизв-е внутренние силовые факторы

При решении многих задач возникает необходимость наряду с удлинениями, обусловленными напряжением, учитывать также удлинения, связанные с температурным воздействием. В этом случае используют способ наложения и деформацию ε рассматривают как сумму силовой деформации и чисто температурной деформации:

ε = σ/Е + αt, где α – коэффициент температурного расширения материала.

Для однородного стержня, нагруженного по концам и равномерно нагретого, получаем:

∆L = PL/EA + Lαt, таким образом, силовая и температурная деформации рассматриваются как независимые.

8. Потенциальная энергия деформации.

Внешние силы, приложенные к твердому телу, совершают работу W. В процессе работы в теле накапливается потенциальная энергия деформированного тела U, кроме того работа идет на сообщение скорости массе тела, т.е. преобразование в кинетическую.

W = U+K

Если нагружение происходит медленно, то и скорость перемещения масс тела будет весьма малой, такой процесс называется статическим, и для него характерно W=U, чтобы определить W необходимо построить график зависимости между приложенной силой F и растяжением ∆L,

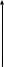F

W

∆L

W=F∆L/2

U=1/2*NNL/EA=N²L/2EA

Если брус состоит из нескольких участков, то общая потенциальная энергия определяется путем суммирования по участкам.

9. Напряжение на наклонных площадках при растяжении-сжатии. Анализ линейного напряженного состояния

Полное напряжение P на наклонной площадке, согласно условию однородности напряженного состояния для всех точек площадки, будет одни и тем же. Р= σ

Раскладывая это напряжение по нормали и по касательной к наклонной площадке, находим

σ_α=Р τ_α=Р

или

σ_α= σ τ_α= σ

При растяжении бруса наклонные сечения, как и поперечные, остаются плоскими и параллельными. Следовательно, внутренние силы распределенны по наклонным сечениям равномерно.

Нормальные напряжения в поперечном сечении растянутого или сжатого стержня есть главное напряжение. Так как отличное от нуля только одно главное напряжение, то напряженное состояние при одноосном растяжении (сжатии) является линейным.

При растяжении:

При сжатии: