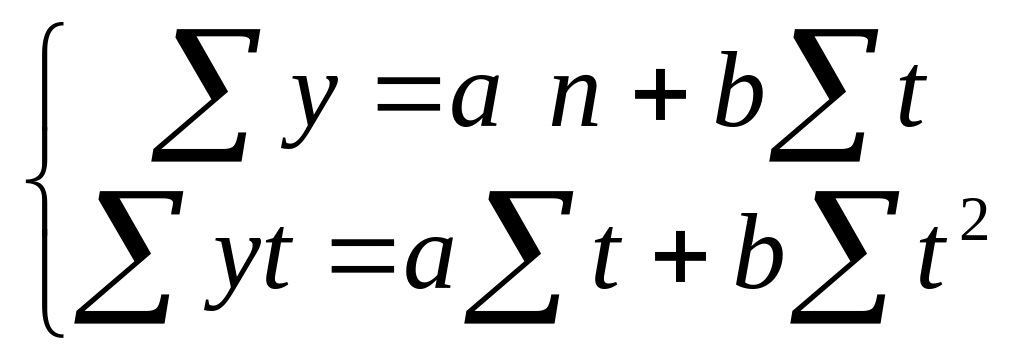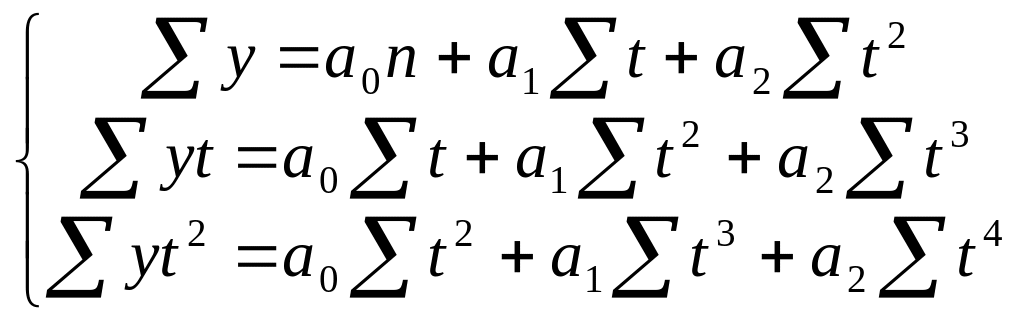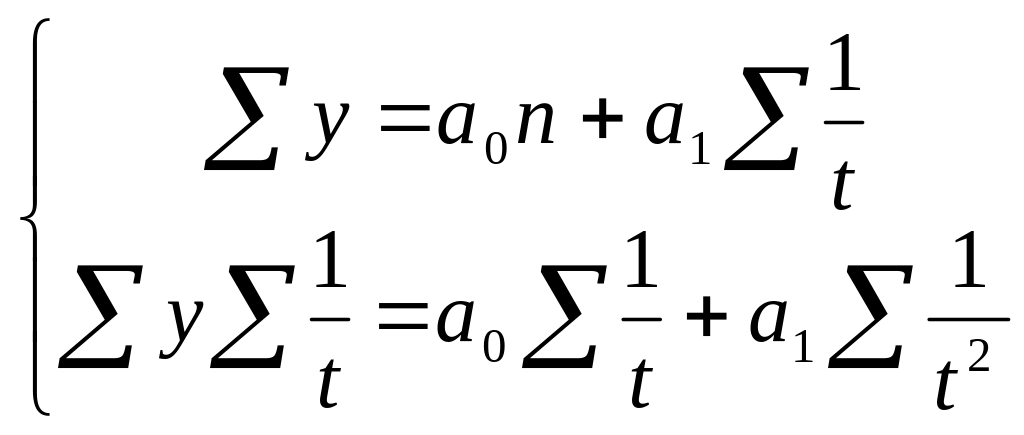5. Виды трендовых моделей для аналитического выравнивания ряда динамики.

Вид уравнения определяется характером динамики развития конкретного явления. Логический анализ при выборе вида уравнения может быть основан на рассчитанных показателях динамики, а именно:

• если относительно стабильны абсолютные приросты (первые разности уровней приблизительно равны), сглаживание может быть выполнено по прямой;

• если абсолютные приросты равномерно увеличиваются (вторые разности уровней приблизительно равны)., можно принять параболу второго порядка;

• при ускоренно возрастающих (замедляющихся) абсолютных приростах – параболу третьего порядка

• при относительно стабильных темпах роста- показательную функцию.

Наименование функции	Вид функции	Система нормальных равнений для нахождения параметров уравнения
Линейная
Парабола второго порядка
Показательная
Гиперболическая

где у_t – значение уровней фактического ряда динамики:

t – временные данные

n – количество уровней ряда динамики.

В динамических рядах значение t почти всегда образует арифметическую последовательность, поэтому, чтобы упростить расчеты, удобно в качестве начала отсчета времени брать середину ряда. Тогда сумма нечетных степеней t будет равна нулю.

Если дан ряд динамики, содержащий нечетное количество уровней (например, 5), то его целесообразно представить в виде:

t = -2, -1, 0, 1, 2;

у = у _-2, у _–1, у₀, у₁, у₂.

Если дан ряд динамики, содержащий четное количество уровней (например, 6), то

t = -5, -3, -1, 1, 3, 5;

у = у _-5, у _-3, у _-1, у₁, у₃, у₅.

Так как при этом Σt = 0, то система нормальных уравнений упрощается:

; Откуда ; .

Нахождение по имеющимся данным за определенный период времени некоторых недостающих значений признака внутри периода называется интерполяцией. Нахождений значений признака за пределами анализируемого периода называется экстраполяцией.

Пример 9. Реализация картофеля на рынках города за три года характеризуется следующими данными, т:

Гот	Месяц
	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII
1995	70	71	82	190	280	472	295	108	605	610	184	103
1996	71	85	84	308	383	443	261	84	630	450	177	168
1997	63	60	59	261	348	483	305	129	670	515	185	104

Определить индексы сезонности.

Решение. Для исчисления индексов сезонности применяют раз личные методы, выбор которых зависит от характера общей тенден ции ряда динамики. Если ряд динамики не содержит ярко выражен ной тенденции развития, то индексы сезонности исчисляют непо средственно по эмпирическим данным без их предварительного вы равнивания. Для расчета индексов сезонности необходимо иметь по месячные данные минимум за три года.

Для каждого месяца рассчитывается средний уровень (J_;), зате! исчисляется среднемесячный уровень для всего анализируемого ряд. uj- По этим данным определяется индекс сезонности (7^) как про рентное отношение средних для каждого месяца к общему средне месячному уровню ряда:

I=U. 100,

У где 17

~' ~~ среднемесячные уровни ряда (по одноименным месяцам);

~- общий средний уровень ряда (постоянная средняя

Применяя формулу средней арифметической проа n>j = —' , определим среднемесячные уровни за три года: I

_ 70 + 71+63 204 _ы январь: у_х =-------;-------= —т- = 68 т;

_ 71 + 85 + 60 216 _. , , <_ J

февраль: у₂ =-------5-------= ~Г" = 72 т и т.д. (см. табл. 5.7, гй

_ 2J/ Исчислим общую (постоянную) среднюю: у =-----=

_ 68 + 72 + 75 + 253 + 337 + 466 + 287 + 107 + 635 + 525 + 182 + 125

_

= 261 т,

или

__ 11. у; 3070 + 3144 + 3182 9396

^у ~ £ щ ~ 12 + 12+12 " 36 ~ ^Т-

Индексы сезонности имеют следующие значения:

со

январь: l_s - -х^у = 0,263, или 26,3%;

72 февраль: I_s = -jrr- 0,276, или 27,6%, и т.д. (см. табл. 5.7, гр

			Реализация			картофеля.		т	Индекся
						Сумма		Среднемесячная	ССЗОННОС1
	1995 г.	1996 г		1997 г.		за три		за три года
						года		Я-	_________
А	1	2		3		4		5
Январь	70	71		63		204		68	26,3 i
Февраль	71	85		60		216		72	27,6 '
Март	82	84		59		225		75	28,7 ■
Апрель	190	308		261		759		253	96,9 ;
Май	280	383		348		1011		337	129,1 i
Июнь	472	443		483		1398		466	178,5|
	7QS	?fii		4ns		»Л1		7Я7	110.0 !

	.—■	2	3	4
A____J		84	129	321	107
Август	605	630	670	1905	635
Сентябрь	610	450	515	1575	525
Октябрь	184	177	185	546	182
Ноябрь		168	104	375	125
1 Дскао££__^	ЧП70	3144	3182	9396	v = 261