V. Анализ частотных распределений. Понятие о закономерностях распределения.
Во многих вариационных рядах распределения можно заметить определенную зависимость между изменением значений варьирующего признака и частот. Частоты могут сначала увеличиваться с увеличением значений признака, а затем в середине ряда уменьшаться. Такие закономерности изменения частот в вариационных рядах называются закономерностями распределения. Одна из важных целей статистического изучения вариационных рядов – это выявить закономерность распределения и определить ее характер.
Изучение формы распределения.
Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариант.
Разновидности кривых распределений.
одновершинные: симметричные, умеренно асимметричные и крайнеасиметричные.
многовершинные кривые
Для однородных совокупностей характерны одновершинные распределения. Многовершинные свидетельствуют о неоднородности изучаемой совокупности.
При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии (As):
или
Если As>0, то правосторонняя асимметрия.
Если As<0, то левосторонняя асимметрия.
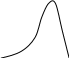
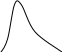
Если As>0,5, то асимметрия значительна.
Если As<0,25, то асимметрия незначительна.
Оценка
существенности As
производится на основе квадратической
ошибки, коэффициента асимметрии
,
,
n – число наблюдений.
Если
,
то асимметрия существенна и распределение
признака в генеральной совокупности
несимметрично, иначе асимметрия
несущественна.
Для симметричных распределений может быть рассчитан показатель эксцесса (Ek)
,
где
центральный момент 4-го порядка
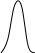
Островершинное распределение
Плосковершинное распределение
Среднеквадратическая ошибка эксцесса (σEk):
,
n – число
наблюдений
Показатели ассиметрии и эксцесса характеризуют непосредственно лишь форму распределения признака в пределах изучаемой совокупности, однако их определение имеет не только описательное значение. Часто асссиметрия и эксцесс дают определенные указания для дальнейшегог исследования социально-экономических явлений.
Например, появление значительного отрицательного эксцесса может указать на качественную неоднородность исследуемой совокупности. Кроме того, эти показатели позволяют сделать вывод о возможности применения данного эмпирического рспределения к типу кривых нормального распределения.
Теоретическое распределения в анализе вариационных рядов.
В статистике широко используются различные виды теоретических распределений: нормальное распределение, биноминальное распределение, распределение Пуассона и др. Каждое из них имеет специфику и свою область применения в различных отраслях знаний. Чаще всего используется нормальное распределение.
,
где
-
ординат кривой нормального распределения;
-
стандартизированное отклонение;
и
-
математические постоянные;
х – варианты вариационного ряда;
-
их средняя величина;
-
среднее квадратическое отклонение.
Нормальное распределение полностью определяется двумя параметрами – средней арифметической и средним квадратическим отклонением. Подчиненность закону нормального распределения проявляется тем точнее, чем больше случайных величин действует вместе. Если ни одна из случайных действующих причин по своему действию не окажется преобладающей над другими, то закон распределения очень близко подходит к нормальному. Такая закономерность проявляется, например, в распределении отклонений в производственном процессе при нормальном уровне организации и технологии. В распределении населения определенного возраста по размеру обуви и т. д.
Объективная характеристика соответствия эмпирического распределения нормальному может быть получена с помощью особых статистических показателей – критериев согласия.