Выборочное наблюдение.

1. Понятие о выборочном наблюдении.

2. Средняя и предельная ошибки выборки.

3. Способы формирования выборочной совокупности.

4. Определение необходимого объема выборки.

5. Оценка результатов выборочного наблюдения.

6. Малая выборка.

1. Понятие о выборочном наблюдении.

Выборочное наблюдение – несплошное наблюдение, при котором статистическому обследованию подвергаются единицы изучаемой совокупности, отобранные случайным образом.

К нему статистика прибегает по следующим причинам:

1. Экономия ресурсов. Пример: существует множество субъектов хозяйственной деятельности (АО, фермерские хозяйства и др.) и их сплошное исследование требует огромных материальных и финансовых затрат.

2. Ускорение получения необходимых данных.

3. Расширение программы наблюдения. Можно более широко и детально изучить отдельные единицы совокупности.

4. Кадровое обеспечение. Выборочное наблюдение позволяет привлекать небольшое количество сотрудников, но более профессиональных.

5. Существуют задачи, которые решаются лишь с помощью методологии выборки. Пример: исследование качества продукции.

6. Возможность его использования в целях уточнения и для разработки данных сплошного наблюдения.

Организационный план проведения выборочного наблюдения

1. Постановка цели и задачи наблюдения.

2. Определение границ объекта исследования.

3. Отработка программы наблюдения и разработка ее материалов.

4. Определение метода, способа отбора и объема выборки.

5. Подготовка кадров, инструктированных документов.

6. Расчет выборочных характеристик и определение ошибок выборки.

7. Распространение выборочных данных на всю совокупность.

Выборочная совокупность – совокупность отобранных для обследования единиц.

Генеральная совокупность – совокупность единиц, из которых производится отбор.

Характеристики выборочной и генеральной совокупностей.

№ п/п	Характеристика	Генеральная совокупность	Выборочная совокупность
1	Объем совокупности	N	n
2	Численность единиц, обладающих обследуемым признаком	M	m
3	Доля единиц, обладающих обследуемым признаком
4	Средний размер признака
5	Дисперсия количественного признака
6	Дисперсия доли

2. Средняя и предельная ошибки выборки.

Существуют средняя и предельная ошибки выборки, которые вычисляются для количественных и качественных признаков.

Средняя ошибка выборки:

Случайный отбор	Для средней	Для доли
повторный отбор
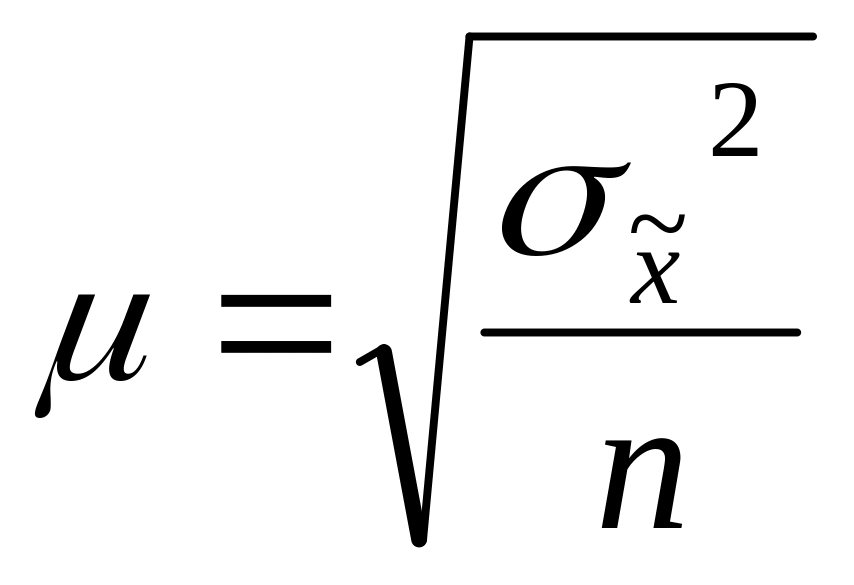
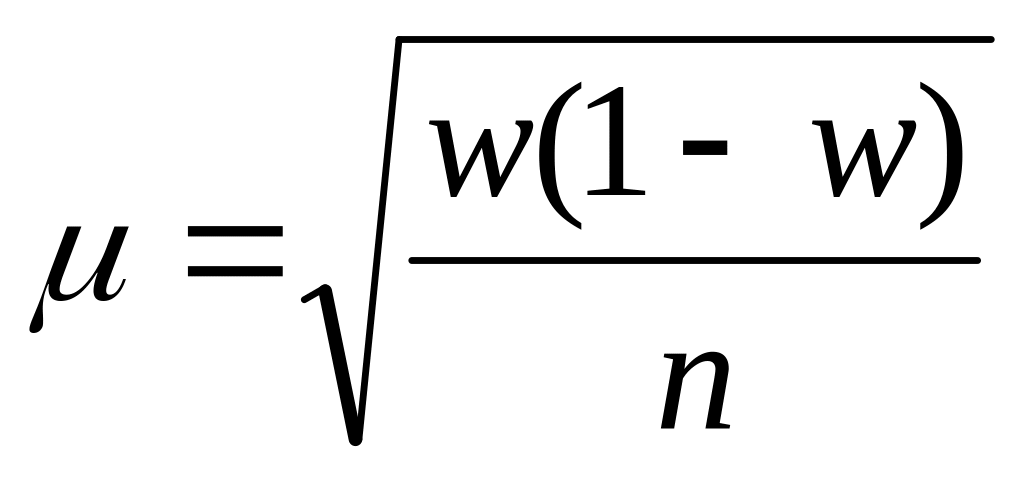
бесповторный отбор

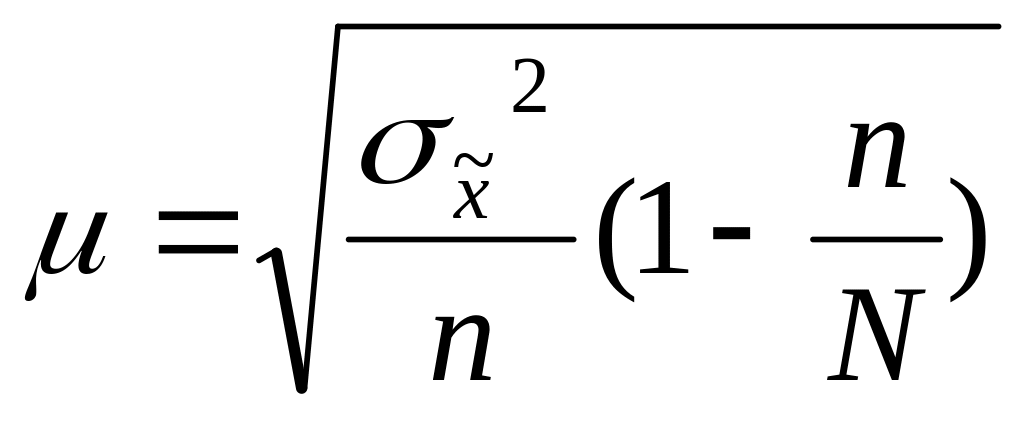
Средняя ошибка выборки показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности.

Предельная ошибка выборки

Для средней , для доли , где

предельная ошибка средней;

-предельная ошибка доли;

- величина средней квадратической ошибки.

t – коэффициент доверия, определяемый в зависимости от уровня вероятности;

Коэффициент доверия вычисляется с помощью функции Лапласа, которые вычислены и приводятся в специальных математических таблицах. В частности, при

t=1 F(t) =0,683 t=2 F(t) =0,954; t=3 F(t) =0,997;

t=1,5 F(t) =0,866; t=2,5 F(t) =0,988; t=3,5 F(t) =0,999;

Формулы предельной ошибки позволяют решать задачи трех видов:

1. Определение интервалов генеральных характеристик с заданной степенью надежности (доверительной вероятностью)

Доверительные интервалы для генеральной средней:

Доверительные интервалы для генеральной доли:

Для различных способов отбора предельная ошибка рассчитывается при проведении выборочного наблюдения по-разному.

2. Определение доверительной вероятности того, что генеральная характеристика может отличаться от выборочной не более чем на определенную заданную величину.

, по величине t определятся доверительная вероятность.