2. Стационарное уравнение Шрёдингера. Решение для одномерной потенциальной ямы.

Оно для того, чтобы найти вероятности местонахождения частицы.

- в общем случае (Е = U(x,y,z,t))

- переход

- стационарное уравнение Шредингера.

Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)

г де l — ширина «ямы», а энергия отсчитывается от ее дна (рис. 296).

Уравнение Шредингера (217.5) для стационарных состояний в случае одномерной задачи запишется в виде

По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. В пределах «ямы» (0 £ х £ l) уравнение Шредингера (220.1) сведется к уравнению или где Общее решение дифференциального уравнения Так как по (220.2) y(0)=0, то В=0. Тогда Условие (220.2) y(l)=A sin kl = 0 выполняется только при kl = np, где n — целые числа, т. е. необходимо, чтобы Из выражений (220.4) и (220.6) следует, что Т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Е_n, зависящих от целого числа п. Следовательно, энергия Е_n частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Е_n называются уровнями энергии, а число п,определяющее энергетические уровни частицы, называется главным квантовым числом. 

Билет 4

1. Принцип суперпозиции. Интерференция световых волн. Разность хода (геометрическая и оптическая), разность фаз. Монохроматичность, когерентность (пространственная и временная). Время когерентности, длина когерентности.

. Интерференция света — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной. Колебания когерентны, если разность их фаз постоянна во времени и при сложении колебаний получается колебание той же частоты.

Продолжительность процесса излучения кванта энергии атомом составляет 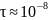с. За это время атом испускает волновой цуг, перемещающийся во времени как единое целое. Интервал времени , в течение которого фаза колебаний остается приблизительно постоянной, называют временем когерентности. В вакууме волна за это время распространяется на расстояние (где – скорость света), называемое длиной когерентности волн (или длиной цуга). Таким образом, длина когерентности есть расстояние, при прохождении которого две или несколько волн утрачивают когерентность. Отсюда следует, что наблюдение интерференции света возможно, если оптическая разность хода .

Оптической длиной пути называется произведение геометрической длины пути световой волны в данной среде на показатель преломления этой среды. Разность оптических длин путей, проходимых волнами, называется оптической разностью хода .

- условие максимумов, - условие минимумов.

Геометрическая разность хода – реальная видимая на картинке, в метрах, а сколько один луч короче.