Оценка сложности
Алгоритм Беллмана-Форда завершает свою работу в течение времени O(V*E), поскольку инициализация в строке 1 занимает время O(V), на каждый из |V| — 1 проходов по ребрам в строках 2-4 требуется время в O(E), а на выполнение цикла for в строках 5-7 — время O(Е).
Выполнение алгоритма Беллмана-Форда:
Н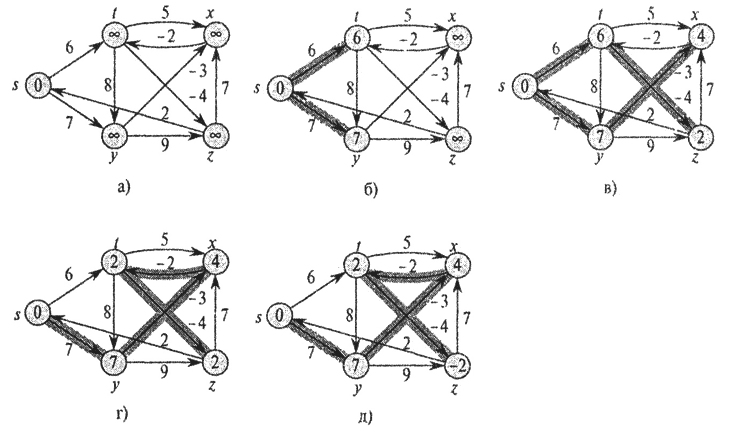
а
рисунке в вершинах графа показаны
значения атрибутов d на
каждом этапе работы алгоритма, а
выделенные ребра указывают на значения
предшественников: если ребро (u, v)
выделено, то prev[v] = u.
В рассматриваемом примере при каждом
проходе ребра ослабляются в следующем
порядке: (t, х), (t, у), (t, z), (x,t), (у,х), (у, z),
(z,x), (z,s), (s,t), (s,y). В части а рисунка показана
ситуация, сложившаяся непосредственно
перед первым проходом по ребрам. В частях
б-д проиллюстрирована ситуация после
каждого очередного прохода по ребрам.
Значения атрибутов d и prev, приведенные
в части д, являются окончательными.
Граф с отрицательными циклами
Алгоритм Беллмана–Форда позволяет очень просто определить, существует ли в графе G отрицательный цикл, достижимый из вершины s. Достаточно произвести внешнюю итерацию цикла не , a ровно |V| раз. Если при исполнении последней итерации длина кратчайшего пути до какой-либо вершины строго уменьшилась, то в графе есть отрицательный цикл, достижимый из s. На основе этого можно предложить следующую оптимизацию: отслеживать изменения в графе и, как только они закончатся, сделать выход из цикла (дальнейшие итерации будут бессмысленны).
С равнительный анализ.
Критерии |
Алгоритм Беллмана — Форда
|
Алгори́тм Де́йкстры |
Работает ли с оринтированными графами? |
+ |
+ |
Есть ли поддержка отрицательных путей? |
+ |
- |
Есть ли поддержка петель? |
- |
- |
Сложность алгоритма |
O(n2) |
O(n2) |
Поддержка циклов |
+ |
+ |
Реализация алгоритма Форда-Беллмана.
PROGRAM Edge;
type
edge = record
start, finish, length: integer;
end;
var
cur: integer;
n, m, v, i, j, t, k: integer;
d: array [0..100] of integer;
p: array [0..100] of integer;
e: array [0..100] of edge;
path: array [0..100] of integer;
const
INF = 1000000000;
begin
writeln('Введите кол-во вершин.');
readln(n);
writeln('Введите номер НАЧАЛЬНОЙ вершины.');
readln(v);
writeln('Введите номер КОНЕЧНОЙ вершины.');
readln(t);
for i:=0 to n-1 do begin
d[i]:=INF;
end;
d[v]:=0;
writeln('Введите кол-во ребер в графе.');
readln(m);
for i:=0 to m-1 do begin
writeln('Введите номер начальной вершины ', i+1, '-го ребра.');
readln(e[i].start);
writeln('Введите номер конечной вершины ', i+1, '-го ребра.');
readln(e[i].finish);
writeln('Введите длину ', i+1, '-го ребра.');
readln(e[i].length);
end;
for i:=0 to n-1 do begin
for j:=0 to m-1 do begin
if ((d[e[j].finish]) < (d[e[j].start] + e[j].length)) then begin
d[e[j].finish]:= d[e[j].finish];
end else begin
d[e[j].finish]:= d[e[j].start] + e[j].length;
p[e[j].finish]:= e[j].start;
end;
end;
end;
writeln('-------------');
if (d[t]=INF) then begin
writeln('No path');
end else begin
//cur:=t;
k:=0;
{
for cur:=t to -1 do begin
path[k]:=cur;
cur:=p[cur];
inc(k);
end;
}
while (cur <> -1) do begin
path[k]:=cur;
cur:=p[cur];
inc(k);
end;
end;
for i:=1 to k do begin
writeln(path[i]);
end;
end.
Вывод: В ходе данной работы были рассмотрены два алгоритма: Алгоритм Форда-Беллмана и Алгоритм Дейкстры. При сравнительном анализе было выявлено, что Алгоритм Форда-Беллмана является более эффективным и реализуемым. Провели практическую реализацию алгоритма.