3.2 Программная реализация транспортной задачи с помощью Delphi 7

Блок – схема программы представлена в приложении 1.

Программа, которая будет представлена дальше, выполнена в системе Delphi 7.[6] Задача выводит допустимое решение, пользователю лишь необходимо ввести с клавиатуры потребности i-го потребителя, затем ввести запасы j-го поставщика. Клавишей «Enter» пользователь вызывает таблицу, в которой отображены вводимые пользователем данные и допустимое решение. Ниже представлен пример (рисунок 6) использования написанной задачи, код самой программы представлен в приложении 2. Программа выдает лишь допустимое решение, оно возможно не является оптимальным.

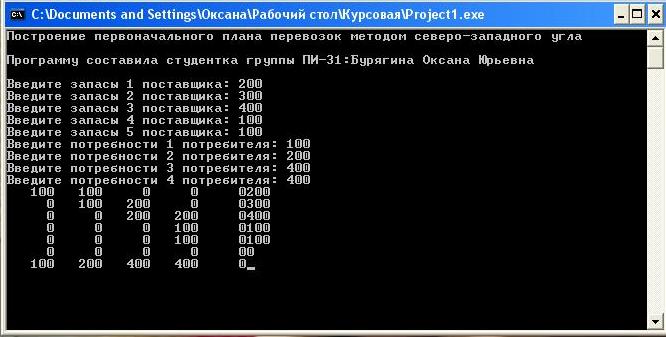
Рисунок 6

Заключение

В данной курсовой работе изложены основные подходы и методы решения транспортной задачи с ограничениями. Решение данной задачи позволяет наиболее рационально формировать план предприятия: минимизировать затраты, максимизировать прибыль, сохранять хорошие отношения между поставщиками и потребителями, разработать наиболее рациональные пути и способы транспортирования товаров, устранить повторные перевозки. Это все очень важно для функционирования предприятия. Таким образом, важность решения данной задачи для экономики предприятия несомненна.

Алгоритм и методы решения транспортной задачи могут быть использованы при решении некоторых экономических задач, не имеющих ничего общего с транспортировкой груза.

В данной курсовой показана программная реализация транспортной задачи с построением первоначального опорного плана северо – западным методом и само решение - методом потенциалов. Программа является не конечным продуктом, ее можно доработать, подстроить под нужное нам количество потребителей и поставщиков. Универсальность данной программы, это ее главный плюс. Решение данной программы возможно и не является оптимальным, но решается пользователем за доли секунд. Таким образом, мы можем гораздо быстрее составить план перевозок и сэкономить время.

Курсовая работа помогла поближе познакомиться с транспортными задачами, и узнать какие же существуют ограничения. Конечно, рассмотреть все существующие ограничения в рамках одной курсовой работы невозможно, но рассмотрены самые основные.

Цель курсовой работы выполнена, посредством поставленных задач.

Список использованных источников:

[1] http://www.grandars.ru/model-transportnoy-zadachi.html

[2] Монахов В.М., Беляева Э.С., Краснер Н.Я. Методы оптимизации. – М.: Просвещение, 1978.

[3] http://ru.wikipedia.org/wiki/Алгоритм_Куна

[4] Глухов В.В., Медников М.Д., Коробко С.Б.. Математические методы и модели для менеджмента.- СПб.:Лань,2007.

[5]http://ru.wikipedia.org/wiki/Транспортная_задача

[6]Фаронов В.В, DELPHI. Программирование на языке высокого уровня: Учебник для ВУЗов-СПб.: Питер,2008.

Приложение 1

нет да

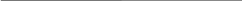
Методом северо-западного угла

Метод потенциалов

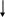Нет Да

Приложение 2

Program Transportnaya;

Uses crt; {подключение модуля очистки экрана}

Const n=6; {количество строк}

m=5; {количество столбцов}

Var a:array [1..n] of integer; {Массив поставщиков}

b:array [1..m] of integer; {Массив потребителей}

a1:array [1..n] of integer; {Дополнительный массив запасов}

b1:array [1..m] of integer; {Дополнительный массив потребностей}

c:array [1..n,1..m] of integer; {Основной массив в который производится запись базисного решения}

i,j,k,x,y,s,p:integer; {Необходимые переменные}

{ввод с клавиатуры}

procedure vvodklav;

begin

i:=1;

k:=0;

s:=0;

while (k=0) and (i<n) do

begin

write('Введите запaсы ',i,' поставщика: ');

readln(a[i]);

if a[i]=0 then

begin

k:=1;

i:=i-1;

end

else

begin

a1[i]:=a[i];

s:=s+a1[i];

i:=i+1;

end;

end;

j:=1;

k:=0;

p:=0;

textcolor(6);

while (k=0) and (j<m) do

begin

write('Введите потребности ',j,' потребителя: ');

readln(b[j]);

if b[j]=0 then

begin

k:=1;

j:=j-1;

end

else

begin

b1[j]:=b[j];

p:=p+b1[j];

j:=j+1;

end;

end;

k:=0;

if s<p then

begin

writeln('Ошибка ввода!!! Проверьте баланс между поставщиками и потребителями');

readln;

halt;

end;

if (p<s) and (k=0) then

begin

writeln('Ошибка ввода!!! Проверьте баланс между поставщиками и потребителями');

readln;

halt;

end;

x:=i;

y:=j;

end;

begin

clrscr; {очистка экрана}

writeln('Построение первоначального плана перевозок методом северо-западного угла');

writeln;

writeln('Программу составила студентка группы ПИ-31:Бурягина Оксана Юрьевна ');

writeln;

vvodklav; {Использование процедуры ввода с клавиатуры}

repeat

k:=0;

if (b[j]-a[i]<0) then

begin

c[i,j]:=b[j];

a[i]:=a[i]-b[j];

b[j]:=0;

j:=j-1;

k:=1;

end;

if (b[j]-a[i]>0) and (k=0) then

begin

c[i,j]:=a[i];

b[j]:=b[j]-a[i];

a[i]:=0;

i:=i-1;

k:=1;

end;

if (b[j]-a[i]=0) and (k=0) then

begin

c[i,j]:=a[i];

a[i]:=0;

b[j]:=0;

i:=i-1;

j:=j-1;

end;

if (i=0) or (j=0) then break;

until false;{Выводим решение}

clrscr;

for i:=1 to x do

begin

for j:=1 to y do

if j=y then write(c[i,j]:6,a1[i])

else

write(c[i,j]:6);

writeln;

end;

for j:=1 to y do

write(b1[j]:6);

readln;

end.