Содержание

Задание №1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

Задание №2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

Задание №3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

Задание №4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

Список литературы………………………………………………….......... 35

Вариант №15 Задание №1

В таблице 1 приведены результаты испытаний 25-ти экземпляров технической системы (значения времени отказа отдельных экземпляров системы ). Номер испытания соответствует номеру исследуемого экземпляра системы.

Используя данные отдельных испытаний в соответствии с вариантом задания провести расчеты и вычисления указанные ниже.

1. Рассчитать показатели надежности испытанной системы:

1. определить оценку средней наработки системы до отказа ;

2. определить оценку среднеквадратического отклонения времени отказа системы ;

3. построить графики зависимости оценки вероятности отказов от времени по результатам испытаний .

2. Подобрать зависимость для фукции распеределения лучше описывающей результаты испытаний:

1. рассчитать значения статистического ряда и привести соответствующую ей гистограмму;

2. найти параметры для экспоненциального закона , апроксимирующих результаты испытания ( );

3. найти параметры усеченного нормального закона ;

4. найти параметры нормального закона , используя «Закон »;

5. привести графики апроксимирующих зависимостей , , ;

6. выбрать более подходящую зависимость (лучше описывающую результаты испытания) используя следующие критерии:

- величину общей суммы квадрата отклонения между значениями полученной оценки функции распределения и апроксимирующим выражением ;

- критерий Колмогорова.

№ испытания	1	2	3	4	5	6	7	8	9	10	11	12
Время отказа	60	88	260	408	523	583	696	753	782	805	880	968

Таблица №1.1

13	14	15	16	17	18	19	20	21	22	23	24	25
1056	1160	1179	1246	1405	1444	1524	1575	1645	1735	1754	1798	2198

Решение

РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ СИСТЕМЫ

Определение средней наработки системы до отказа .

К числу показателей надежности невосстанавливаемых систем, являющихся числовыми характеристиками случайных величин, относится средняя наработка до отказа (среднее время безотказной работы) – математическое ожидание случайной величины Т наработки до отказа (или времени безотказной работы). При этом статистическая оценка до отказа:

= ,

где t_i – время отказа i-го экземпляра системы;

N – количество экземпляров; N = 25.

= (60+ 88+ 260 + 408 + 523 + 583+ 696 + 753 + 782 + 805 + 880+ 968 + 1056 + 1160 + 1179 + 1246 + 1405 + 1444 + 1524 + 1575 + 1645+ 1735 + 1754 + 1798+ 2198) / 25 = 26525/ 25 = 1061 час

Определение оценки среднеквадратического отклонения времени отказа системы .

,

где t_i – время отказа i-го экземпляра системы;

- оценка средней наработки до отказа. ( = 1061 час);

N – количество экземпляров; (N = 25.)

,

= = = 560, 73 час

Построение графиков зависимости оценки вероятности отказов от времени по результатам испытаний .

Статистическая оценка вероятности отказа Q(t) при фиксированном значении t = t₁:

N = 25,

Таблица 1.2

	1/25	2/25	3/25	4/25	5/25	6/25	7/25	8/25	9/25	10/25	11/25	12/25	13/25
t, час	60	88	260	408	523	583	696	753	782	805	880	968	1056
	14/25	15/25	16/25	17/25	18/25	19/25	20/25	21/25	22/25	23/25	24/25	25/25
t, час	1160	1179	1246	1405	1444	1524	1575	1645	1735	1754	1798	2198

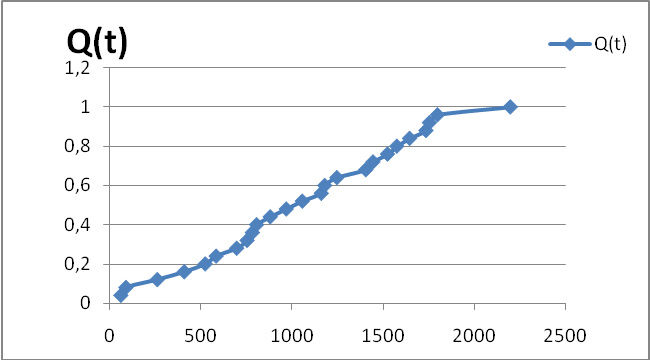
Рисунок 1.1 – Зависимость оценки вероятности отказов Q(t) от времени t

ПОДБОР ЗАВИСИМОСТИ ДЛЯ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

Расчет значений статистического ряда и построение соответствующей ему гистограммы.

Δt = 438 час, таблица исходных данных для построения гистограммы приведена:

t+Δt	N(t+Δt)
0-438	4
438-876	6
876-1341	6
1341-1752	6
1752-2190	3

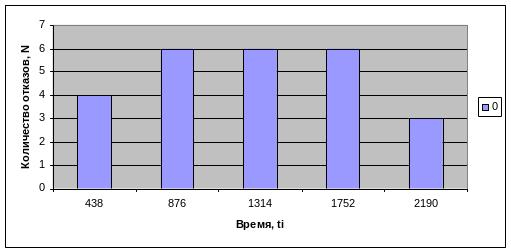
Рисунок 1.2 - Распределение количества отказов во времени

Расчет параметров для экспоненциального закона , апроксимирующих результаты испытания ( ). Функция распределения имеет вид: F (t) = 1 – e ^{- λt}

Оценка интенсивности отказов равна:

,

где - оценка средней наработки до отказа, которая найдена в п.п 1.1 ( ); Тогда

.

Таким образом: F (t) = 1 –

Нахождение параметров усеченного нормального закона

При усеченном нормальном законе распределения наработки системы до отказа

,

где t_max – время отказа последнего экземпляра; t_max = 2198 час;

;

из закона 3 оценка среднеквадратического отклонения равна:

.

Найти параметры нормального закона

При нормальном законе распределения наработки системы до отказа

Оценка среднеквадратического отклонения времени отказа системы , вычисленная в п.п. 1.2, равна = 560,73 час

Графики апроксимирующих зависимостей , , ;

— Рассчитаем вероятность отказа системы в момент времени t

для экспоненциального закона распределения наработки системы до отказа.

Функция распределения имеет вид: F (t) = 1 –

— Рассчитаем оценку вероятности отказа системы в момент времени t для нормального закона распределения наработки системы до отказа.

Функция распределения наработки системы до отказа имеет вид:

= НОРМРАСП (x; m; σ; тип) = НОРМРАСП (t; 1061; 560,73; 1)

— Рассчитаем оценку вероятности отказа системы в момент времени t для нормального усеченного закона распределения наработки системы до отказа

= (НОРМРАСП (t; m; ; тип) - F (0))·С ₁, где

С₁ – нормирующий множитель, С₁ = 1/(1 - F (0))

F (0) = НОРМРАСП (0; 1099; 366, 4; 1) = 0,001352

С₁ = 1/(1- F (0)) = 1/(1- 0,001352) = 1,001352

= (НОРМРАСП(t; 1099;366,4; 1) - 0,001352)·1,001352

Результаты приведены в таблице:

Таблица 1.3

t
60	0,054952	0,000936	0,037117
88	0,079553	0,001547	0,041349
260	0,217233	0,009676	0,076575
408	0,319097	0,028339	0,1221
523	0,389005	0,056694	0,168663
583	0,42258	0,078275	0,196979
696	0,480886	0,134519	0,257544
753	0,508024	0,171382	0,291405
782	0,521282	0,192379	0,309395
805	0,531543	0,210092	0,323998
880	0,563497	0,274036	0,373426
968	0,598222	0,35948	0,434135
1056	0,630185	0,452547	0,496443
1160	0,664697	0,565524	0,570071
1179	0,670645	0,585857	0,583338
1246	0,690789	0,655397	0,629272
1405	0,733801	0,797909	0,730222
1444	0,743403	0,826564	0,752709
1524	0,762029	0,876794	0,795516
1575	0,773192	0,902917	0,82034
1645	0,787665	0,931817	0,851178
1735	0,804925	0,958643	0,885319
1754	0,808385	0,963033	0,89175
1798	0,816165	0,971748	0,905637
2198	0,873879	0,998644	0,978705

Графики апроксимирующих зависимостей:

—◊— - Оценка вероятности отказов Q(t)

—o— - Экспоненциальный закон распределения

—Δ— - Нормальный закон распределения

—□— - Нормальный усеченный закон распределения

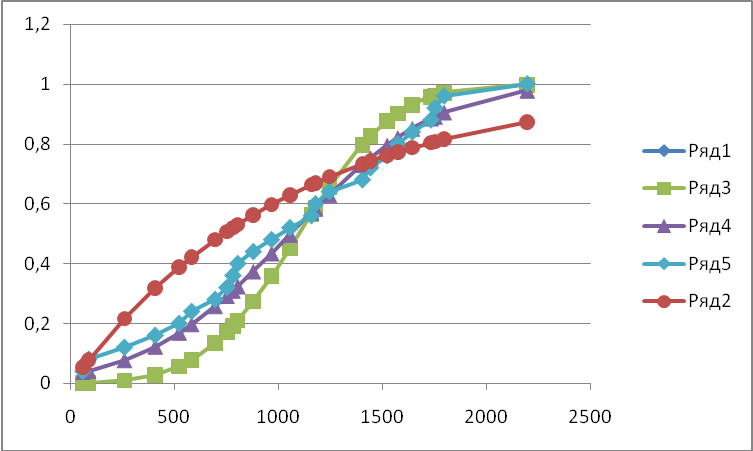
Рисунок 1.3 – Графики аппроксимирующих зависимостей

Выбирается более подходящая зависимость (лучше описывающую результаты испытания) используя следующие критерии:

1) Величину общей суммы квадрата отклонения между значениями полученной оценки функции распределения и апроксимирующим выражением , где Q(t_i) – оценка вероятности отказа системы к моменту времени t_i, полученная из опытных данных;

F(t_i) – оценка вероятности отказа системы к моменту времени t_i, полученная из аппроксимирующей зависимости.

— Для экспоненциального закона распределения наработки системы до отказа S_эксп= = (0,05495 – 0,04)² +…+ (0,873 – 1)² = 0,0159

— Для нормального закона распределения наработки системы до отказа

S_норм = = (0,0009 – 0,04)² + … + (0,9986 – 1)² = 1,84·10^-6

— Для нормального усеченного закона распределения наработки системы до отказа S_{норм. ус.} = = (0,03712 – 0,04)² + … + (0,9787 – 1)² = 0,000453477

Как видно, S_{норм. ус.} > S _норм > S _эксп, то есть самым неточным для описания результатов испытания является нормальный усеченный закон распределения наработки системы до отказа, а наиболее точным – экспоненциальный закон, наряду с нормальным, поскольку их общие суммы квадрата отклонения между значениями полученной оценки функции распределения и апроксимирующим выражением близки по значениям друг к другу.

2) Критерий Колмогорова.

По критерию Колмогорова показатель отклонения равен:

Д = max (abs( - ))

-	-	-
-0,01495	0,039064	0,002883
0,000447	0,078453	0,038651
-0,09723	0,110324	0,043425
-0,1591	0,131661	0,0379
-0,18901	0,143306	0,031337
-0,18258	0,161725	0,043021
-0,20089	0,145481	0,022456
-0,18802	0,148618	0,028595
-0,16128	0,167621	0,050605
-0,13154	0,189908	0,076002
-0,1235	0,165964	0,066574
-0,11822	0,12052	0,045865
-0,11019	0,067453	0,023557
-0,1047	-0,00552	-0,01007
-0,07065	0,014143	0,016662
-0,05079	-0,0154	0,010728
-0,0538	-0,11791	-0,05022
-0,0234	-0,10656	-0,03271
-0,00203	-0,11679	-0,03552
0,026808	-0,10292	-0,02034
0,052335	-0,09182	-0,01118
0,075075	-0,07864	-0,00532
0,111615	-0,04303	0,02825
0,143835	-0,01175	0,054363
0,126121	0,001356	0,021295

Выбираем максимальное значение для каждого из законов:

Д = max (abs( - )) = 0,2008

Д = max (abs( - )) = 0,1899

Д = max (abs( - )) = 0,0760

Аналогично сравнению по величине общей суммы квадрата отклонения, самым точным для аппроксимации результатов испытания является экспоненциальный закон распределения наработки системы до отказа и близкий к нему нормальный закон, а самым неточным – нормальный усеченный закон.