2.2 Расчет надежности системы приближенными методами

Метод минимальных путей и минимальных сечений является приближенным методом расчета надежности невосстанавливаемых систем сложной структуры.

Метод минимальных путей позволяет находить оценку вероятности безотказной работы сверху.

В данной схеме можно рассмотреть много путей, ограничимся путями с количеством элементов не более 3:

1) 8, 9

2) 1, 2, 3

3) 1, 13, 9

8

9

1

2

3

1

13

9

Рисунок 2.12 - Схема для расчета оценки вероятности безотказной работы сверху

Расчет вероятности безотказной работы сверху:

= 1-(1-0,83 0,94) (1-0,94 0,86 0,89) (1-0,94 0,83 0,94)= 0,984

Метод минимальных сечений позволяет находить оценку вероятности безотказной работы снизу. В данной схеме возможны сечения с количеством элементов 3, 4, 5 и более, ограничимся числом элементов не более 3:

1. 9, 2, 11

2. 8, 1, 10

3. 9, 13, 12

Рисунок 2.13 - Схема для расчета оценки вероятности безотказной работы снизу

Расчет вероятности безотказной работы снизу:

=(1-(1-0,94)(1-0.86)(1-0,87))(1-(1-0,83)(1-0,94)(1-0,95))(1-(1-0,94)(1-0,83)(1-0,91)) = =0,997

Задание 3

На заданной территории расположен опасный объект, развитие аварийных ситуаций для которого характеризуется деревом сценариев (см. рисунок).

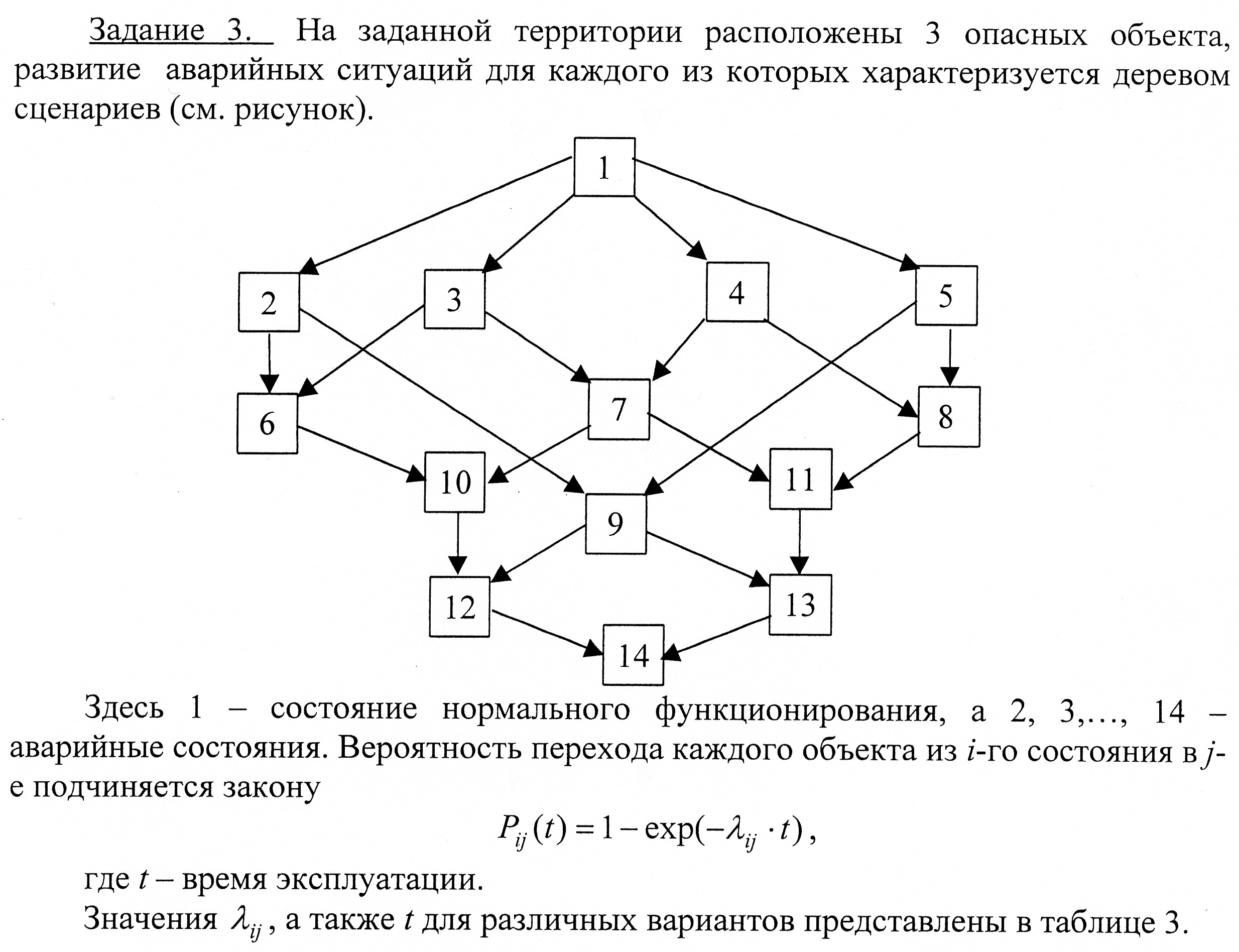
Рисунок 3.1 – Дерево событий

Здесь 1 – состояние нормального функционирования, а 2, 3,…, 14 – аварийные состояния. Вероятность перехода каждого объекта из i-го состояния в j-е подчиняется закону ,

где t – время эксплуатации (для различных вариантов значения представлены в таблице 4), – интенсивность отказов для вероятности перехода объекта из i-го состояния в j-е состояние (для различных вариантов представлены в таблице ). t =680 часов

Таблица 3.1 λ_ij, *10^-5 час^-1

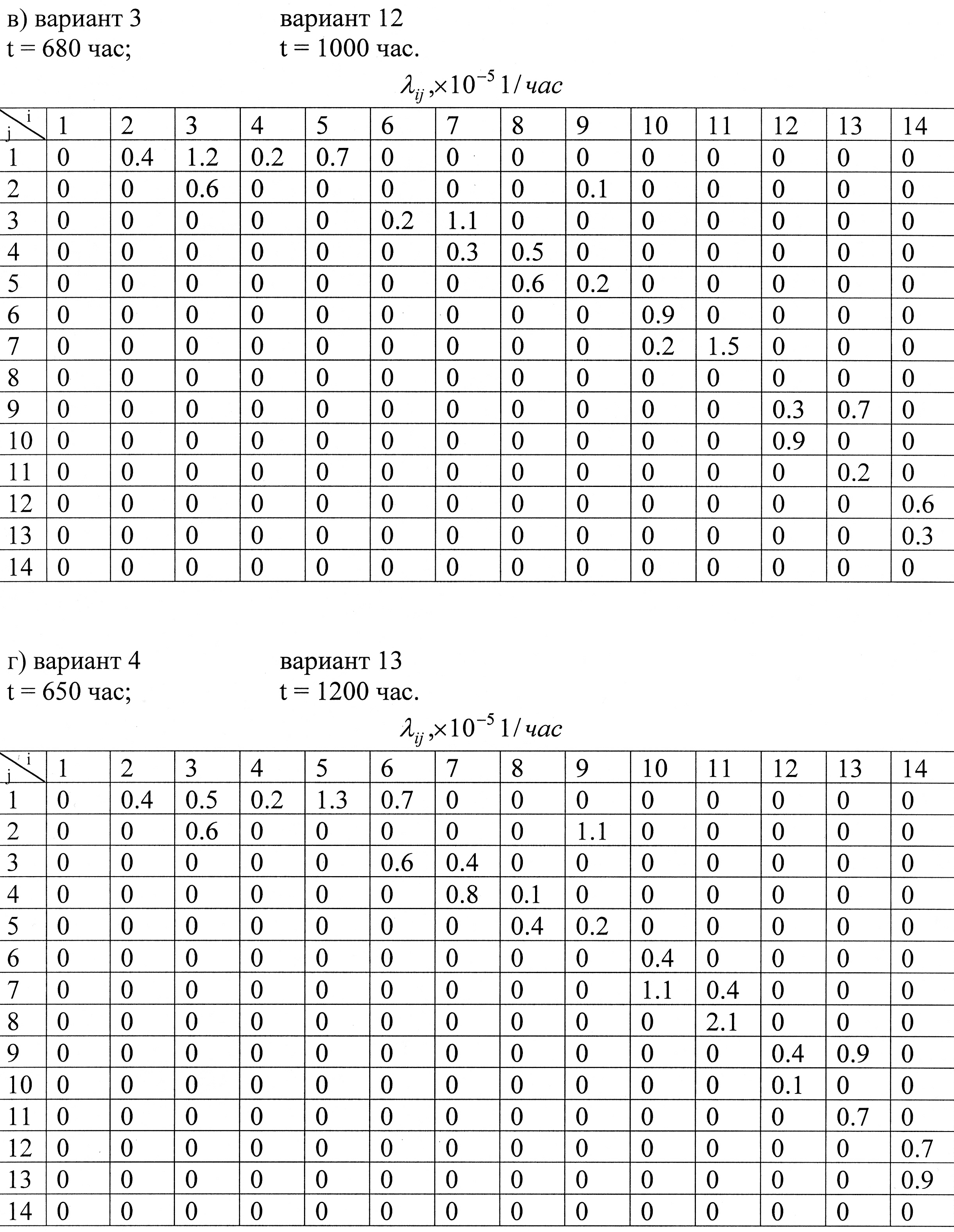
Функция распределения ожидаемого числа пострадавших для каждого i-го состояния подчиняется нормальному закону. В таблице приводятся значения с.к.о. и вероятности того, что число пострадавших не превысит 1000 человек. Величину математического ожидания M_i последствий можно найти по указанным значениям, используя метод подстановки или с помощью замены переменной и использования табличных значений функции Лапласа.

Таблица 3.2

Для нормального состояния функционирования (состояния номер 1) последствия не учитываются.

Найти величину показателя риска R (среднюю величину ожидаемых потерь).

Показатель риска R равен:

,

где Q_i – ожидаемое число погибших для i-го состояния;

Р'_i – вероятность возникновения i-го состояния.

Расчет вероятности перехода из i-го состояния в j-ое производят по формуле:

,

где t – время эксплуатации, t = 680 часов;

λ_ij – интенсивность отказов для вероятности перехода объекта из i-го состояния в j-ое состояние.

Таблица 3.3 – Вероятности перехода из i-го состояния в j-тое.

	2	3	4	5	6	7	8	9	10	11	12	13	14
1	0,00272	0,00813	0,00136	0,00475	0	0	0	0	0	0	0	0	0
2	0	0	0	0	0,00407	0	0	0,00136	0	0	0	0	0
3	0	0	0	0	0,00136	0,00745	0	0	0	0	0	0	0
4	0	0	0	0	0	0,00204	0,00339	0	0	0	0	0	0
5	0	0	0	0	0	0	0,00407	0,00136	0	0	0	0	0
6	0	0	0	0	0	0	0	0	0,00610	0	0	0	0
7	0	0	0	0	0	0	0	0	0,00136	0,00101	0	0	0
8	0	0	0	0	0	0	0	0	0	0,00136	0	0	0
9	0	0	0	0	0	0	0	0	0	0	0,00204	0,00475	0
10	0	0	0	0	0	0	0	0	0	0	0,00610	0	0
11	0	0	0	0	0	0	0	0	0	0	0	0,00136	0
12	0	0	0	0	0	0	0	0	0	0	0	0	0,00407
13	0	0	0	0	0	0	0	0	0	0	0	0	0,00204

Расчет вероятности возникновения i-го состояния:

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

.

Ожидаемое число погибших подчиняется нормальному закону:

,

где σ – среднеквадратическое отклонение;

Р(x) – вероятность того, что число погибших не превысит х человек.

Методом перебора с помощью встроенной функции НОРМРАСП в программе Microsoft Excel находим математическое ожидание:

Таблица 3.4

Состоя-ние, i	2	3	4	5	6	7	8	9	10	11	12	13	14
σi	7	5	8	3	7	6	2	7	4	9	11	4	5
Р(1000)	0,9	0,7	0,89	0,4	0,8	0,7	0,79	0,9	0,7	0,67	0,7	0,53	0,4
Mi, чел.	991	997	990	1000	993	996	998	991	997	996	994	999	1001

Математическое ожидание M_i соответствует ожидаемому числу погибших Q_i в i-ом состоянии (i = 2,3,…,14).

Следовательно, показатель риска равен:

В случае возникновения аварийной ситуации погибнет 17 человек.