2.1 Расчет надежности системы точным методом

Данная схема не сводится к последовательно-параллельной, следовательно, это система сложной структуры. Расчет надежности можно произвести методом разложения относительно особого элемента. Этот метод основан на использовании формулы полной вероятности:

,

где P{H_i} – вероятность того, что особый элемент находится в состоянии H_i;

P{A/Hi} – вероятность состояния А при условии, что особый элемент находится в состоянии H_i.

Выберем группу особых элементов: №5, №6, №13. В таком случае рассмотрим 8 гипотез надежности системы:

Таблица 2.2

№	5	6	13	P{Hi}
1	0	0	0	0,002499
2	0	0	1	0,012201
3	0	1	0	0,033201
4	0	1	1	0,162099
5	1	0	0	0,045899
6	1	0	1	0,000735
7	1	1	0	0,124899
8	1	1	1	0,609801

Гипотеза 1

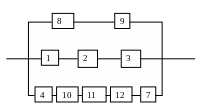
Рисунок 2.2 - Схема соединения элементов системы в смысле надежности в случае возникновения гипотезы Н₁

Вероятность наступления гипотезы Н₁: ;

Формулы для расчета вероятности безотказной работы системы при условии наступления гипотезы Н₁:

Р1,2,3=Р1Р2 Р3=0,94 0,86 0,89=0,719476

Р8,9 = Р8Р9 =0,83 0,94=0,7802

Р_4,7,10,11,12== Р4Р7 Р10 Р11Р12 =0,85 0,94 0,95 0,87 0,91=0,60094

= 1–(1–0,719476)·(1– 0,7802)

(1–0,60094) = 0,97539

Гипотеза 2

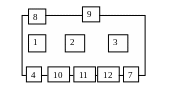
Рисунок 2.3 - Схема соединения элементов системы в смысле надежности в случае возникновения гипотезы Н₂

Вероятность наступления гипотезы Н₂:

Формулы для расчета вероятности безотказной работы системы при условии наступления гипотезы Н₂:

Р_4,7,10,11,12=Р₄Р₇Р₁₀ Р₁₁Р₁₂=0,85 0,94 0,95 0,87 0,91=0,60094

Р_2,3,9=1-(1-Р₉ )( 1-Р₂ Р₃ )=1-( 1-0,94 )( 1-0,86 0,89 )=0,9859

Р_1,8=1-( 1-Р₁ )( 1-Р₈ )=1-( 1-0,94 )( 1-0,83 )=0,9898

= 1– (1 – 0,9859·0,9898)·(1 – 0,60094) = 0,99036

Гипотеза 3

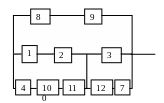
Рисунок 2.4 - Схема соединения элементов системы в смысле надежности в случае возникновения гипотезы Н₃

Вероятность наступления гипотезы Н₃:

Формулы для расчета вероятности безотказной работы системы при условии наступления гипотезы Н₃:

Р8,9 = Р8Р9 =0,83 0,94=0,7802

Р_1,2,4,10,11=1-( 1-Р₁ Р₂ )( 1-Р₄Р₁₀ Р₁₁ )=1-(1-0,94 0,86)(1-0,85 0,95 0,87)=0,943

Р_3,7,12=1-( 1-Р₃)(1-Р₇Р₁₂)=1-(1-0,89)(1-0,94 0,91)=0,984

Р_{1,2,3,4,7,10,11,12}= Р_1,2,4,10,11 Р_3,7,12=0,943 0,984=0,928

= 1-(1-0,7802)(1-0,928)= 0,984

Гипотеза 4

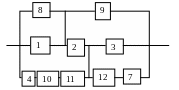
Рисунок 2.5 - Схема соединения элементов системы в смысле надежности в случае возникновения гипотезы Н₄

Вероятность наступления гипотезы Н₄:

Данная схема не сводится к последовательно-параллельной, следовательно, это сложная структура. Расчет надежности можно произвести методом повторного разложения относительно особого элемента 2.

Рассмотрим 2 гипотезы:

Н₁₍₂₎- элемент работоспособен;

Н₂₍₂₎- элемент неработоспособен

Рисунок 2.6 - Схема соединения элементов системы в смысле надежности в случае возникновения гипотезы Н_{4 и} Н₁₍₂₎

Вероятность возникновения гипотезы Н₁₍₂₎ при условии возникновения гипотезы Н₄:

Р{Н₁₍₂₎}=Р₂ Р{Н₄}=0,86 0,162099=0,1394

Формулы для расчета вероятности безотказной работы системы при условии наступления гипотезы Н₅:

Р_8,1,4,10=1-( 1-Р₈)(1-Р₁)(1-Р₄Р₁₀ Р₁₁)=1-(1-0,83)(1-0,94)(1-0,85 0,95 0,87)= =0,997

Р_9,3,7,12=1-( 1- Р₉ )( 1- Р₃)(1-Р₇Р₁₂)=1-(1-0,94)(1-0,89)(1-0,94 0,91)=0,999

=0,997 0,999= 0,996

Рисунок 2.7 - Схема соединения элементов системы в смысле надежности в случае возникновения гипотезы Н_{4 и} Н₂₍₂₎

Вероятность возникновения гипотезы Н₂₍₂₎ при условии возникновения гипотезы Н₄:

Р{Н₂₍₂₎}= Q₂ Р{Н₄}=(1-0,86) 0,162099=0,02269

Р_1,8=1-( 1-Р₁ )( 1-Р₈ )=1-( 1-0,94 )( 1-0,83 )=0,9898

Р_3,7,12=1-( 1-Р₃)(1-Р₇Р₁₂)=1-(1-0,89)(1-0,94 0,91)=0,984

Р{А/Н₂₍₂₎}=1-(1-Р_1,8 Р₉)(1-Р_3,7,12 Р4Р10 Р11)=1-(1-0,9898 0,94)(1-0,984 0,85 0,95 0,87)=0,9785

Формулы для расчета вероятности безотказной работы системы при условии наступления гипотезы Н₅:

· + · = 0,1394·0,996+ 0,02269·0,9785= 0,161045

Гипотеза 5

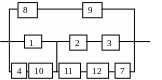
Рисунок 2.8 - Схема соединения элементов системы в смысле надежности в случае возникновения гипотезы Н₅

Вероятность наступления гипотезы Н₅:

Формулы для расчета вероятности безотказной работы системы при условии наступления гипотезы Н₅:

Р8,9 = Р8Р9 =0,83 0,94=0,7802

Р_1,4,10=1-(1-Р₁)(1-Р₄Р₁₀)=1-(1-0,94)(1-0,85 0,95)=0,988

Р_2,3,7,11,12=1-( 1- Р₂Р₃)(1-Р₇ Р₁₁Р₁₂)=1-(1-0,86 0,89)(1-0,94 0,87 0,91)=0,94

1 – (1 - Р8,9)(1 - Р_1,4,10 Р_2,3,7,11,12) = 1-(1-0,7802)(1-0,988 0,94)=0,984

Гипотеза 6

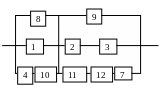
Рисунок 2.9 - Схема соединения элементов системы в смысле надежности в случае возникновения гипотезы Н₆

Вероятность наступления гипотезы Н₆:

Формулы для расчета вероятности безотказной работы системы при условии наступления гипотезы Н₆:

Р_8,1,4,10=1-( 1-Р₈)(1-Р₁)(1-Р₄Р₁₀)=1-(1-0,83)(1-0,94)(1-0,85 0,95)=0,998

Р_{9,2,3,7,11,12}=1-( 1- Р₉ )( 1- Р₂Р₃)(1-Р₇Р₁₁Р₁₂)=1-(1-0,94)(1-0,86 0,89)(1-0,94 0,87 0,91)=0,9964

=0,998 0,9964= 0,9944

Гипотеза 7

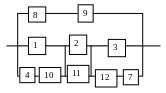
Рисунок 2.10 - Схема соединения элементов системы в смысле надежности в случае возникновения гипотезы Н₇

Вероятность наступления гипотезы Н₇:

Формулы для расчета вероятности безотказной работы системы при условии наступления гипотезы Н₇:

Р_2,11=1-( 1- Р₂ )( 1- Р₁₁ )=1-(1-0,86)(1- 0,87)=0,9818

Р_1,4,10=1-(1-Р₁)(1-Р₄Р₁₀)=1-(1-0,94)(1-0,85 0,95)=0,98845

Р_3,7,12=1-( 1-Р₃)(1-Р₇Р₁₂)=1-(1-0,89)(1-0,94 0,91)=0,984

Р8,9 = Р8Р9 =0,83 0,94=0,7802

1-( 1- Р_8,9 )( 1- Р_1,4,10Р_2,11 Р_3,7,12 )= 1-(1-0,7802)(1-0,98845 0,9818 0,984)=0,99

Гипотеза 8

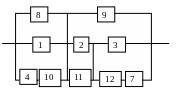
Рисунок 2.11 - Схема соединения элементов системы в смысле надежности в случае возникновения гипотезы Н₈

Вероятность наступления гипотезы Н₈:

Формулы для расчета вероятности безотказной работы системы при условии наступления гипотезы Н₈:

Р_2,11=1-( 1- Р₂ )( 1- Р₁₁ )= 1-(1-0,86)(1- 0,87)=0,9818

Р_8,1,4,10=1-( 1-Р₈)(1-Р₁)(1-Р₄Р₁₀)= 1-(1-0,83)(1-0,94)(1-0,85 0,95)=0,998

Р_3,7,12=1-( 1-Р₃)(1-Р₇Р₁₂)= 1-(1-0,89)(1-0,94 0,91)=0,984

Р_{2,11,3,7,12,9}=1-( 1- Р₉ )( 1- Р_2,11 Р_3,7,12 )=1-(1-0,94)(1-0,9818 0,984)=0,998

=0,998 0,998= 0,996

Вероятности наступления гипотез Н_i предварительно рассчитаны и занесены в таблицу 2.2.

Формулы для расчета вероятности безотказной работы системы:

· + … + · = 0,002499·0,97539+ … + 0,609801·0,996=