1.2.3 Нахождение параметров усеченного нормального закона
При усеченном нормальном законе распределения наработки системы до отказа
,
где tmax – время отказа последнего экземпляра; tmax = 2131 час;
;
из закона 3
оценка среднеквадратического отклонения
равна:
.
1.2.4 Найдем параметры нормального закона
При нормальном законе распределения наработки системы до отказа
Оценка среднеквадратического отклонения времени отказа системы , вычисленная в п.п. 1.2, равна = 507,46 час
1.2.5 Графики апроксимирующих зависимостей , , ;
— Рассчитаем вероятность отказа системы в момент времени t
для экспоненциального закона распределения наработки системы до отказа.
Функция распределения имеет вид: F (t) = 1 –
— Рассчитаем оценку вероятности отказа системы в момент времени t для нормального закона распределения наработки системы до отказа.
Функция распределения наработки системы до отказа имеет вид:
= НОРМРАСП (x; m; σ; тип) = НОРМРАСП (t ; 1132,25; 507,46; 1)
— Рассчитаем оценку вероятности отказа системы в момент времени t для нормального усеченного закона распределения наработки системы до отказа
= (НОРМРАСП (t; m; ; тип) - F (0))·С 1, где
С1 – нормирующий множитель, С1 = 1/(1 - F (0))
F (0) = НОРМРАСП(0; 1065,5; 355,17; 1) = 0,00135
С1 = 1/(1- F (0)) = 1/(1- 0,00135) = 1,00135
= (НОРМРАСП( t; 1065,5; 355,17; 1) - 0,00135)·1,00135
Результаты приведены в таблице:
Таблица 1.3
t |
|
|
|
423 |
0,310811 |
0,08111 |
0,033922 |
654 |
0,437588 |
0,172984 |
0,122124 |
675 |
0,447886 |
0,183779 |
0,134612 |
785 |
0,498825 |
0,246896 |
0,213771 |
876 |
0,537394 |
0,306791 |
0,295876 |
894 |
0,544664 |
0,319358 |
0,313668 |
1078 |
0,612733 |
0,457432 |
0,51338 |
1125 |
0,628423 |
0,494301 |
0,565935 |
1432 |
0,716391 |
0,722635 |
0,848735 |
1624 |
0,76048 |
0,833738 |
0,942001 |
1890 |
0,810468 |
0,93231 |
0,989853 |
2131 |
0,846688 |
0,975474 |
0,998646 |
Графикиапроксимирующих зависимостей:
—
—
- Оценка вероятности
отказов Q(t)
—o— - Нормальный закон распределения
—Δ— - Нормальный усеченный закон распределения
—□— - Экспоненциальный закон распределения
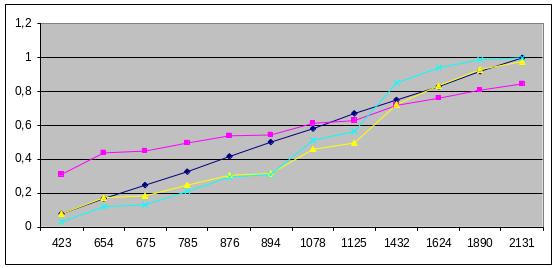
Рисунок 1.3 – Графики аппроксимирующих зависимостей
1.2.6 Выберем более подходящую зависимость (лучше описывающую результаты испытания) используя следующие критерии:
1) Величина общей суммы квадрата отклонения между значениями полученной оценки функции распределения и апроксимирующим выражением , где Q(ti) – оценка вероятности отказа системы к моменту времени ti, полученная из опытных данных;
F(ti) – оценка вероятности отказа системы к моменту времени ti, полученная из аппроксимирующей зависимости.
— Для
экспоненциального закона распределения
наработки системы до отказа Sэксп=
=
(0,310811–
0,08)2
+ … + (0,846688–
1)2
=
=0, 252578
— Для нормального закона распределения наработки системы до отказа
Sнорм
=
= (0,08111–
0,08)2
+ … + (0,975474–
1)2
= =0,104158
— Для нормального
усеченного закона распределения
наработки системы до отказа Sнорм.
ус. =
=
(0,033922–
0,08)2
+ … + (0,998646–
1)2
= 0,123807
Как видно, S эксп. > Sнорм. ус > S норм, то есть самым неточным для описания результатов испытания является экспоненциальный закон распределения наработки системы до отказа, а наиболее точным – нормальный закон.
2) Критерий Колмогорова.
Д = max
(abs(
-
))
Таблица 1.4
-
№
-
-
-
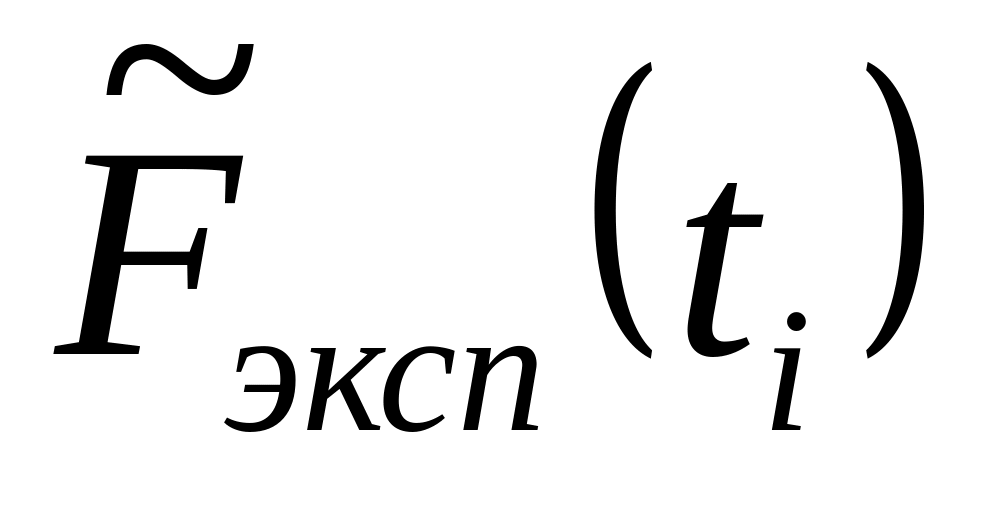
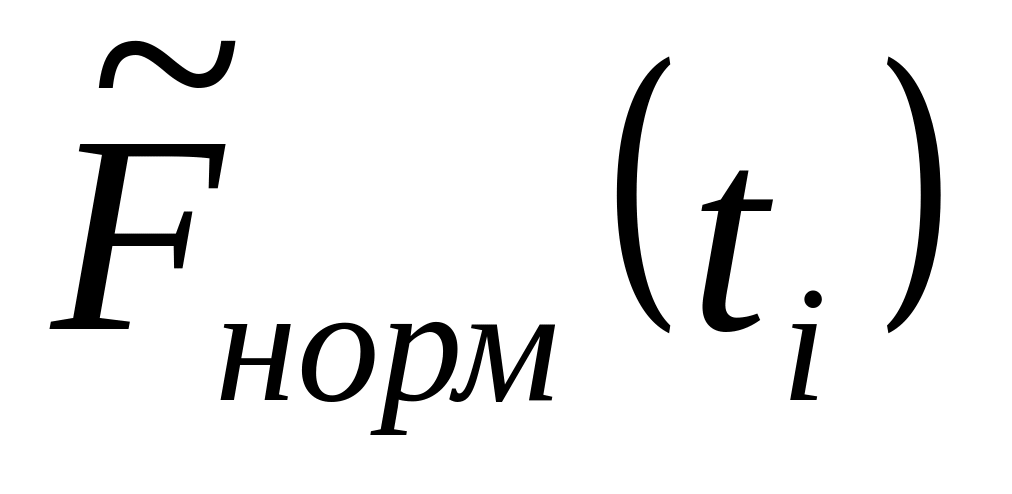
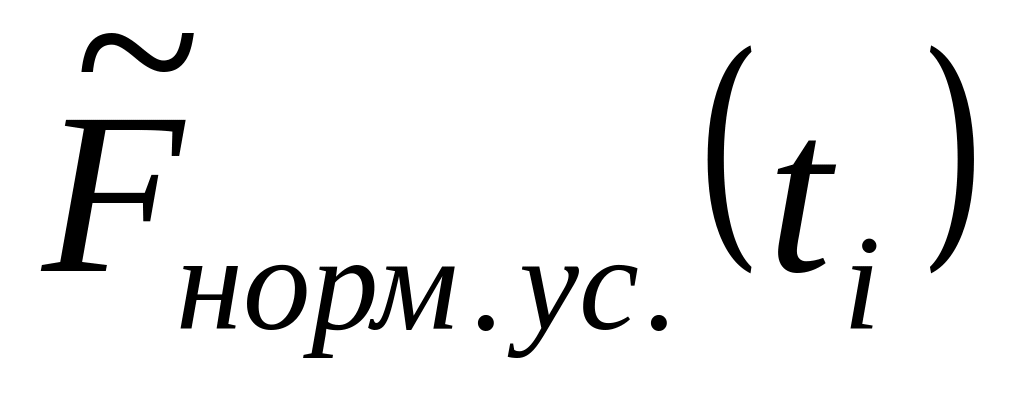
1
-0,23081
-0,00111
0,046078
2
-0,26759
-0,00298
0,047876
3
-0,19789
0,066221
0,115388
4
-0,16883
0,083104
0,116229
5
-0,11739
0,113209
0,124124
6
-0,04466
0,180642
0,186332
7
-0,03273
0,122568
0,06662
8
0,041577
0,175699
0,104065
9
0,033609
0,027365
-0,09873
10
0,06952
-0,00374
-0,112
11
0,109532
-0,01231
-0,06985
12
0,153312
0,024526
0,001354
Д = max (abs( - )) = 0,267588
Д = max (abs( - )) = 0,180642
Д = max (abs( - )) = 0,186332
Как видно, аналогично сравнению по величине общей суммы квадрата отклонения, самым точным для аппроксимации результатов испытания является нормальный закон распределения наработки системы до отказа, а самым неточным – экспоненциальный закон.
Задание 2
Дана схема соединения элементов системы в смысле надежности (номер рисунка соответствует номеру варианта).
Вероятности безотказной работы элементов Pi, i=1,2,…13, приведены в табл. 2.
Требуется произвести расчет надежности:
а) каким-либо точным методом (по выбору);
б) приближенными методами: минимальных путей и минимальных сечений.
Таблица 2.1
-
i
1
2
3
4
5
6
7
8
9
10
11
12
13
Pi
0.94
0.86
0.89
0.85
0.79
0.93
0.94
0.83
0.94
0.95
0.87
0.91
0.83
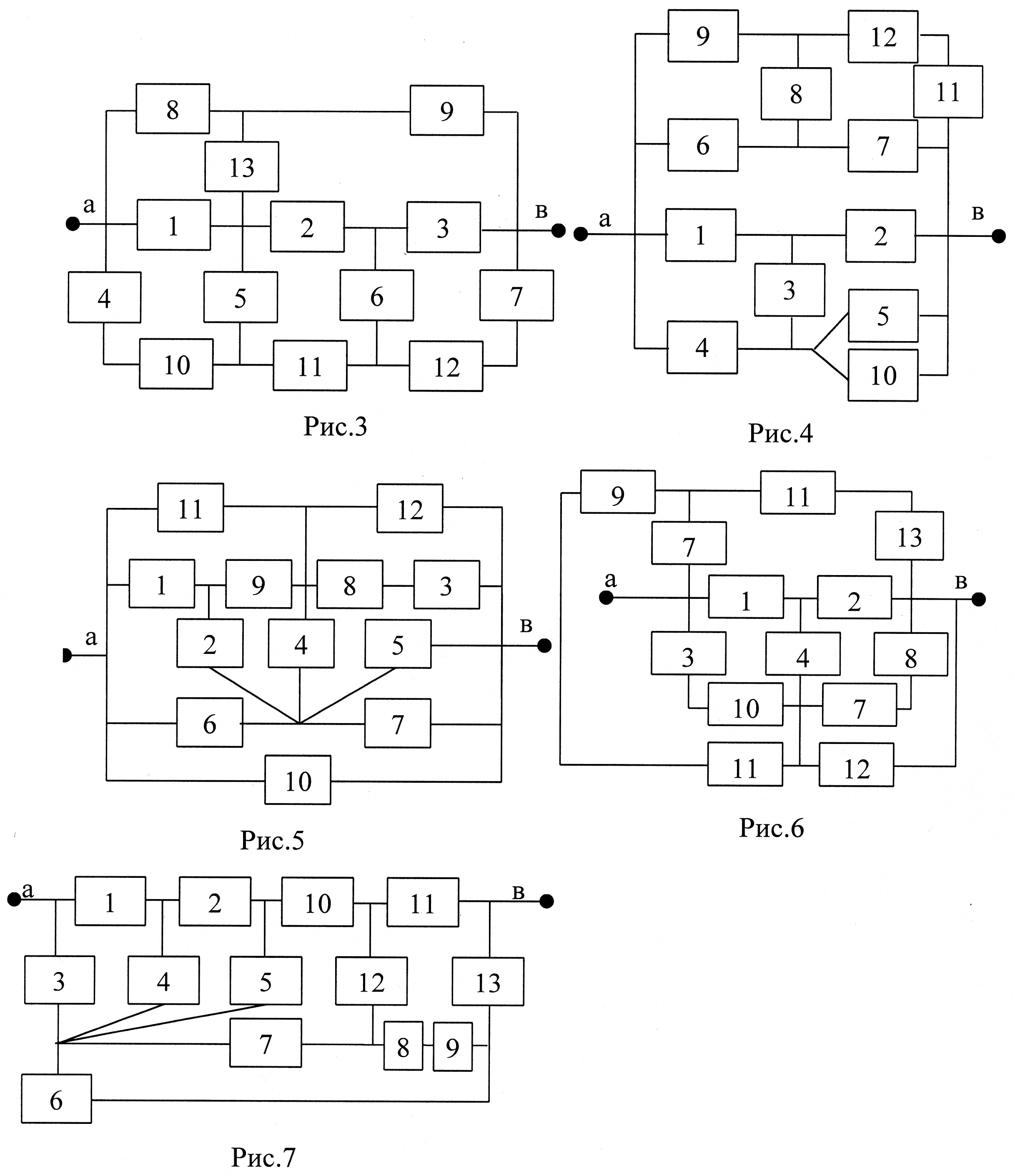
Рисунок 2.1 - Схема соединения элементов системы в смысле надежности
Решение