Опытные и расчетные данные

№ п/п	n, 1/мин	Круп-ность разделения d, м	Вязкость среды, μ, Паּс	Плотность среды ρ, кг/м3	Плотность частиц ρт, кг/м3	Ar	Re	R, м	Кр	ωос, м/с	ωос, ц м/с

Контрольные вопросы

1. Что такое фактор разделения?

2. Что такое крупность разделения?

3. Как рассчитать скорость осаждения частиц в центрифуге?

4. Что такое автомодельный режим?

5. Как найти скорость осаждения частиц нешарообразной формы?

6. Чем отличается свободное осаждение от стесненного?

Лабораторная работа 2

Изучение термического сопротивления теплообменника

Ц е л ь р а б о т ы – изучение на лабораторной модели термического сопротивления теплообменника.

1. Теоретические сведения

Процессы, скорость протекания которых определяется скоростью подвода или отвода тепла, называют тепловыми процессами, а аппаратуру, предназначенную для проведения этих процессов, называют теплоиспользующей аппаратурой.

Основной характеристикой теплового процесса является количество передаваемого в процессе тепла (Q), а основным размером теплового аппарата – поверхность теплообмена. Связь между количеством передаваемого в аппарате тепла и поверхностью теплообмена (F) определяется основным уравнением теплопередачи:

d Q = KΔt dF dτ (15)

или для установившегося процесса и единицы времени это уравнение имеет вид

Q = K Δt_ср F, (16)

где Q – количество переданного тепла через поверхность теплообмена, Вт; K – коэффициент теплопередачи между средами, Вт/(м²К); F – площадь поверхности теплопередачи, м²; Δt – средняя разность температур между средами (движущая сила процесса), К.

В случае кожухотрубного теплообменника процесс теплопередачи от горячей воды к холодной осуществляется согласно схеме (рис. 2), а переход тепла будет выражаться следующими уравнениями:

от горячей воды к поверхности стенки трубы

d Q = ; (17)

переход тепла через стенку трубы (собственной стенки и ржавчины на ней)

d Q = ; (18)

переход тепла от наружной поверхности стенки к холодной воде

d Q = . (19)

В уравнениях (17) – (19) Q – количество передаваемого тепла, Вт; t_ст.н, t_ст.в – температура наружной и внутренней поверхности трубы, °С; r₁, r₂ – термическое сопротивление при переходе тепла соответственно от горячей воды к внутренней поверхности и от наружной поверхности к холодной воде, м²·°С/Вт; ∑r_ст – сумма термических сопротивлений слоев, из которых состоит стенка, м² °С/Вт.

Уравнения (17) –(19) представляем в виде уравнения теплопередачи:

d Q = , (20)

где R = r₁ + ∑r_ст + r₂ есть общее термическое сопротивление при переходе тепла от горячей воды к холодной воде.

При расчетах используют вместо r₁ и r₂ обратные величины:

α₁ = 1/r₁; α₂ = 1/r₂,

где α₁ и α₂ – коэффициенты теплопередачи, соответственно для горячей и холодной воды, Вт/(м²°С). В этом случае уравнения (17) и (19) принимают вид:

dQ = α₁(T – t_ст.в) dF ; (21)

dQ = α₂(t_ст.н. – t) dF ; (22)

Величину, обратную общему термическому сопротивлению R, называют коэффициентом теплопередачи:

K = 1/R = 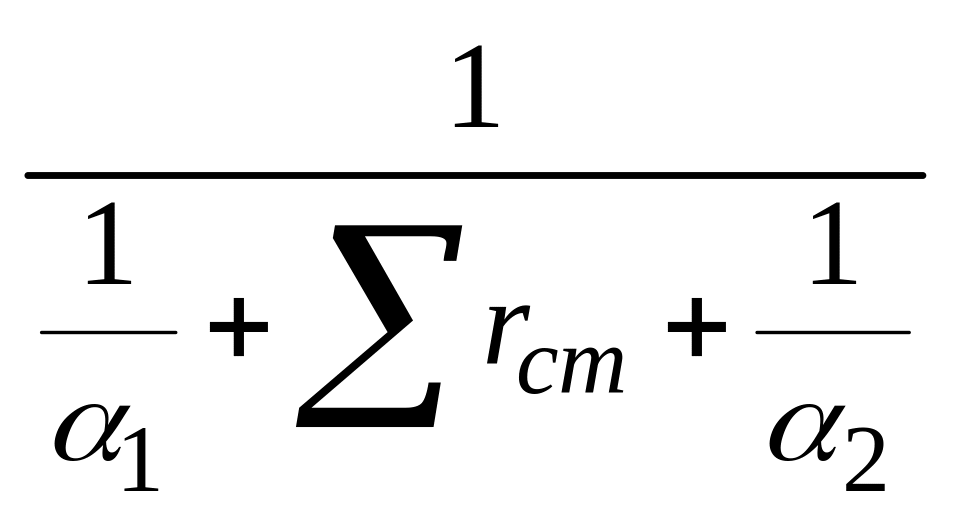(23)

Средняя движущая сила процесса Δt_ср теплопередачи в уравнении (16) для теплообменника есть средняя разность температур горячей и холодной воды, определяемая формулой

Δt_ср = 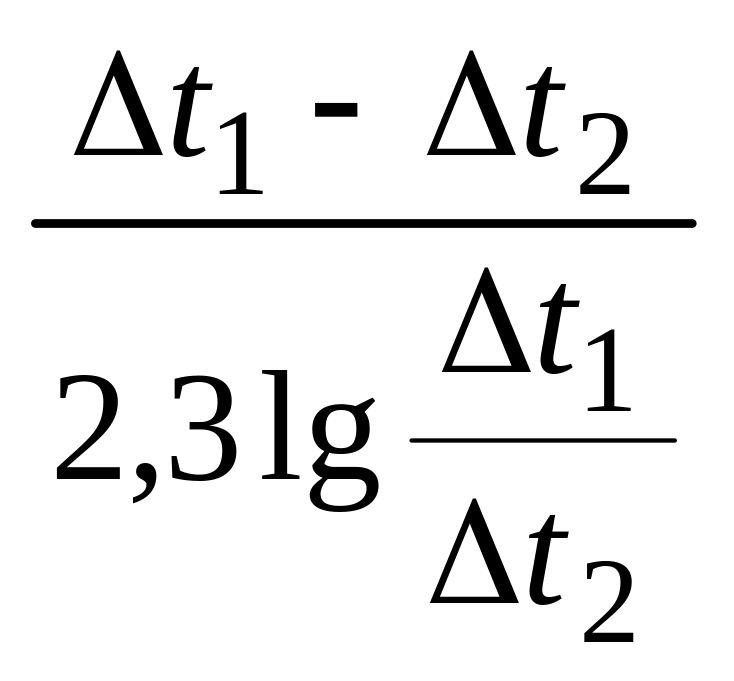, (24)

где Δt₁ = t_н – t_к ; Δt₂ = t'_к - t'_н ; t_н, t_к – начальная и конечная температура горячей воды, ºС; t'_н, t'_к – начальная и конечная температура холодной воды, °С, (т.е. движущие силы на концах теплообменника).

Если , то Δt_ср= . (25)

Расход тепла Q в уравнении (16) рассчитывают по формуле

Q = V·ρ·C(t_к – t_н), (26)

где V – расход воды, м³/с; ρ – плотность воды, кг/м³; С – теплоемкость воды, Дж/(кг °С).

Переход тепла от стенки к протекающей среде (воде) осуществляется через пограничный слой (за счет теплопроводности), а от пограничного слоя в массу (ядро) жидкости (путем конвекции). Этот процесс может быть выражен через систему критериев подобия. Характер критериальной зависимости существенно связан с режимом движения жидкости.

Так, для развитого турбулентного течения жидкости. Когда критерий Рейнольдса Re > 10 000 и отношение длины трубы L к ее внутреннему диаметру L/d ≥ 50, расчетное критериальное уравнение имеет вид

Nu = 0,023 Re^0,8 · Pr^0,5 . (27)

При переходном режиме движения 2300 < Re < 10000 критериальное уравнение выражается так:

Nu = 0,00069 Re^1,24 · Pr^0,5 , (28)

где

Nu = - критерий Нуссельта; (29)

Re = - критерий Рейнольдса; (30)

Pr = - критерий Прандтля; (31)

где α – коэффициент теплоотдачи, Вт/(м²·°С); d – внутренний диаметр трубы, м; λ – коэффициент теплопроводности жидкости, Вт/(м·°С); W – скорость жидкости в трубах, м/с; ρ – плотность жидкости, кг/м³; μ – динамический коэффициент вязкости жидкости, (Па с); с – теплоемкость жидкости, Дж/(кг·°С).

Скорость жидкости определяют через ее расход:

W = V/(0,785·n·d² ), (32)

тогда критерий Рейнольдса (Re):

Re = , (33)

где n – количество трубок в теплообменнике, d –диаметр труб, м; V – расход жидкости, м³/с.