
- •Подготовка инструментария к компьютерной обработке
- •Получение и анализ таблиц очр
- •Команды преобразования данных
- •Проверка статистических гипотез в spss
- •Дисперсионный анализ
- •Двухфакторный дисперсионный анализ
- •Графическое представление данных
- •Построение и анализ таблиц сопряжённости
- •Корреляционный анализ
- •Регрессионный анализ
- •Множественная линейная регрессия
- •Двухфакторный дисперсионный анализ
- •Социологические индексы как инструмент анализа данных
- •Компьютерная обработка пилотажного исследования
- •Построение вс. Определение ошибки выборки и расчёт ди
- •Оформление аналитической записки по результатам статистической обработки данных
- •Классификация многомерных методов анализа данных
- •Семинары
Дисперсионный анализ
- метод, используемый для изучения влияния различных, одновременно действующих и независимых признаков-факторов на изменчивость одного или нескольких зависимых признаков. Условия:
1) независимый признак-фактор – всегда качественная переменная (группирующая);
2) зависимый признак – всегда количественная переменная;
3) зависимая переменная должна распределяться по Нормальному Закону. Замечание: метод устойчив к нарушению нормальности распределения;
4) количество наблюдений в каждой группе должно быть одинаковым. Замечание: метод устойчив к нарушению.
Для ДА характерна внутренняя терминология.
Если присутствует один признак-фактор в качестве независимого – однофакторный; два – двухфакторный и так далее.
H0: µ1 = µ2 = µk = µ(const) среднее значение совпадает с константой.
H1: µk ≠ µ(const) Среднее значение не совпадает хотя бы для некоторых групп.
Фиксировались потери веса у людей, соблюдающих 4 разные диеты. Признак-фактор:
1) белковая;
2) фруктовая;
3) кефирная;
4) раздельное питание.
Зависимый признак – потеря веса в кг за 3 недели.
Предполагалось, что на потерю веса влияет вид диеты.
x = факторA
y =
Для проверки гипотезы используется модель разделения дисперсии зависимой переменной, согласно которой дисперсия зависимой переменной складывается из 2-х составляющих: дисперсии, порождённой признаком-фактором и дисперсией, порождаемой другими причинами внутри каждого уровня фактора. В результате появляется возможность оценки вклада каждой компоненты в изменчивость зависимого признака. Для этого мы должны составить F-отношение.
S2общ = S2мгр + S2вгр
S2общ – общая дисперсия S2мгр – межгрупповая дисперсия (порождённая признак-фактором)
S2вгр – внутригрупповаяя дисперсия (порождённые другими причинами внутри каждого уровня фактора)
*Формула дисперсии*. В ДА вычисляется только числитель – «сумма квадратов»: SS.
SS2общ = SS2мгр + SS2вгр
SS2общ = SSА + SSост
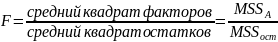

dfA = k – 1 (количество значений признаков фактора)
SSA
=

кол-во респондентов на каждом уровне факторов
 – среднее арифметическое на каждом
уровне факторов
– среднее арифметическое на каждом
уровне факторов
 – общее среднее для всех значений y
– общее среднее для всех значений y

dfост = n – k;
n – объём ВС;
k – число уровней фактора.
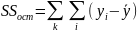
 – конкретное значение зависимой
переменной y на определённые уровни
факторов.
– конкретное значение зависимой
переменной y на определённые уровни
факторов.
 - среднеарифметическое для каждого
уровня факторов.
- среднеарифметическое для каждого
уровня факторов.
Критическая точка – распределение Фишера
Команда One-Way ANOVA
Analyze ---> Compare Means ---> One-Way ANOVA
Dependent List –перенос зависимой переменной.
Factor – перенос независимой переменной.
Options:
Descriptive – дискриптивных или описательных статистик.
Homogeneity of variance test – тест проверки гомегенности дисперсий.
Means plot – график средних.
Post Hoc:
Bonferroni = Tukey, кроме графика подобий.
Tukey – сравнение каждой независимой переменной с другой.
Duncan
H0: µД1 = µД2 = µД3 = µД4 = const
H1: µi ≠ const для некоторых 1=1,4
Дисперсии гомогенны, если извлекаются из одной выборки.
Sig = 0,752 > α = 0,05 => H0 – дисперсии гомогенны.
|
Sum of Squares |
df |
Mean Square |
F |
Sig |
Between Groups |
18,232 |
3 |
6,077 |
5,739 |
0,005 |
Within Groups |
23,296 |
22 |
1,059 |
|
|
Total |
41,528 |
25 |
|
|
|
Sig = 0,005 < α = 0,01 => H1
Следовательно, мы можем утверждать, что вид диеты влияет на интенсивность потери веса. Влияние статистически значимо.
Экспериментальные данные.
