1.Равнобедренный треугольник. Треугольник называется равнобедренным, если у него две стороны равны. Эти стороны называются боковыми, а третья сторона – основанием. Св-ва: В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. Признаки: Если в треугольнике два угла равны, то он равнобедренный. Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.

2.Признаки равенства треугольников. 1. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 2. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. 3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны. Признаки равенства прямоугольных треугольников. 1. По гипотенузе и катету. 2. По гипотенузе и острому углу. 3. По двум катетам. 4. По катету и прилежащему острому углу.

3. Параллельные прямые — это две непересекающиеся прямые, лежащие в одной плоскости. Признаки: 1.Если накрест лежащие углы, образованные при пересечении двух прямых секущей, равны, то прямые параллельны. 2.Если соответственные углы, образованные при пересечении двух прямых секущей, равны, то прямые параллельны. 3.Если односторонние углы, образованные при пересечении двух прямых секущей, в сумме дают 180, то прямые параллельны. Св-ва: 1.Если прямые параллельны, то накрест лежащие углы, образованные при пересечении их секущей, равны. 2.Если прямые параллельны, то соответственные углы, образованные при пересечении их секущей, равны. 3.Если прямые параллельны, то односторонние углы, образованные при пересечении их секущей, в сумме составляют 180.

4. Сумма углов треугольника равна 180 градусов. Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине. Cв-во: Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. Сумма внешних углов n-угольника, взятых по одному при каждой его вершине, равна 360.

5. Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. Св-ва: В параллелограмме противоположные стороны равны и противоположные углы равны. Диагонали параллелограмма точкой пересечения делятся пополам. Углы, прилежащие к любой стороне, в сумме равны 180. Диагонали параллелограмма делят его на два равных треугольника. Биссектриса параллелограмма отсекает от него равнобедренный треугольник. В параллелограмме угол между биссектрисами углов, прилежащих к одной стороне – прямой. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Признаки: Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм. Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм. Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

6.Прямоугольником называется параллелограмм, у которого все углы прямые. Св-ва: Все свойства параллелограмма. Диагонали равны. Признаки: Параллелограмм является прямоугольником, если: 1.Один из его углов прямой. 2.Его диагонали равны.

7. Ромб — параллелограмм, у которого все стороны равны. Все свойства параллелограмма. Св-ва: Диагонали ромба взаимно перпендикулярны. Диагонали ромба являются биссектрисами углов. В ромб всегда можно вписать окружность. Признаки: Если в параллелограмме диагонали взаимно перпендикулярны, то этот параллелограмм — ромб. Если в параллелограмме диагонали являются биссектрисами углов, то этот параллелограмм — ромб.

8. Трапеция — четырехугольник, у которого две стороны параллельны, а две другие — нет. Теорема о четырех точках трапеции. Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой. Св-ва: В равнобедренной трапеции углы при любом основании равны. В равнобедренной трапеции длины диагоналей равны. Признаки: Если трапецию можно вписать в окружность, то она равнобедренная. Около равнобедренной трапеции можно описать окружность. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

9. Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

S =	1	a · h
	2

Формула Герона

S = √p(p - a)(p - b)(p - c)

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

S = p· r

Площадь квадрата равна квадрату длины его стороны.

S = a²

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b

Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h

Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S= a·h Площадь ромба равна половине произведению длин его диагоналей.

S =	1	d1 · d2
	2

Площадь трапеции равна произведению полусуммы ее оснований на высоту 

S =	1	(a+ b) · h
	2

10. Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

11. Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. 

Если биссектриса внешнего угла C треугольника ABC пересекает продолжение противолежащей стороны AB, то BD/AD=BC/AC

12. Отношение площадей 2 подобных треугольников равно квадрату коэффициента подобия.

Площади треугольников, имеющих равные стороны, относятся как соответствующие этим сторонам высоты.

Площади треугольников, имеющих равные высоты (общую высоту), относятся как стороны, соответствующие этим высотам.

Площади треугольников, имеющих равный угол (или общий угол), относятся как произведения сторон, содержащих этот угол.

13. Признаки подобия треугольников:

1) Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

2) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

3) Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

14. Средняя линия — отрезок, соединяющий середины двух сторон этой фигуры. Понятие употребляется для следующих фигур: треугольник, четырехугольник, трапеция.

Средняя линия треугольника:

Средняя линия треугольника параллельна третьей стороне и равна её половине.

При проведении всех трёх средних линий образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.

Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четверти площади исходного треугольника.

Средняя линия трапеции:

Средняя линия параллельна основаниям и равна их полусумме.

Теорема Вариньона:

Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.

15. Свойства прямоугольного треугольника:

Сумма двух острых углов прямоугольного треугольника равна 90º

Катет прямоугольного треугольника, лежащий против угла в 30º, равен половине гипотенузы

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30º.

Пропорциональные отрезки в прямоугольном треугольнике:

1. Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.

2. Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

16. Теорема о пропорциональных отрезках в треугольнике:

Теорема Чевы:

Если на сторонах АВ, ВС и СА треугольника АВС взяты соответственно точки С₁, А₁ и В₁, то отрезки АА₁, ВВ₁ и СС₁ пересекаются в одной точке тогда и только тогда, когда

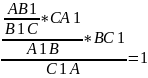
Верно и обратное.

Теорема Менелая:

Если на сторонах АВ и ВС и продолжении стороны АС (либо на продолжениях сторон АВ, ВС и АС) взяты соответственно точки С₁, А1, В1, то эти точки лежат на одной прямой тогда и только тогда, когда

Верно и обратное.

17. Синус, косинус, тангенс, котангенс:

Синус - это отношение противолежащего катета к гипотенузе

Косинус - это отношение прилежащего катета к гипотенузе

Тангенс - это отношение противолежащего катета к прилежащему

Котангенс - то отношение прилежащего катета к противолежащему

Их значения:

Угол	30	45	60
sin x
cos x
tg x
ctg x