4.3. Петли цифровой фапч

Петли цифровой и аналоговой ФАПЧ имеют много общего. Поэтому далее будут представлены только выражения, необходимые для анализа и расчета петель цифровой ФАПЧ, структурная схема одной из которых приведена на рис.4.9.

Рис.4.9. Структурная схема петли цифровой ФАПЧ.

Выходная частота ГУН делится на N₂ и транспонируется в область рабочих частот ДПКД с коэффициентом деления N, т.е. является функцией частоты сравнения f_φ и частоты f_вх:

f_вых= N₂(N f_φ+ f_вх)

При изменении N ДПКД f_вых изменяется ступенями по N₂Nf_φ или ступенями по N₂∙∆f_вх, если f_вх изменяется ступенями по ∆f_вх .В качестве ФД используется ЧФД рис.1.8 или НЧ (десятки кГц) дискретный ФД типа «выборка с запоминанием» (Рис. 4.9') с диапазоном изменения фазы ≈ ±π и подавлением на выходе f_φ не менее, чем на 80дБ.

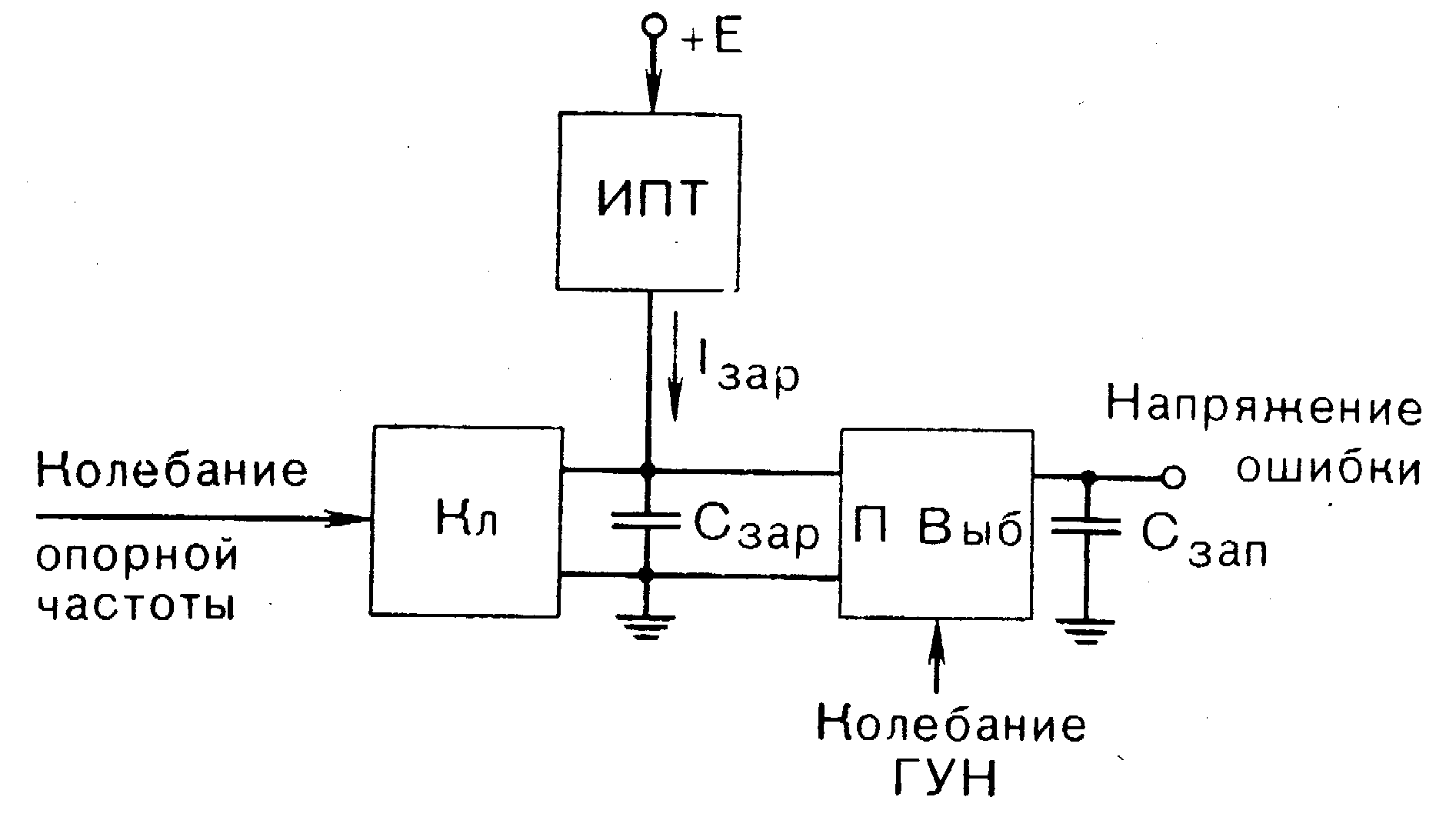
Рис. 4.9'. Структурная схема и напряжения для ФД типа «выборка с запоминанием».

Компенсирующий пропорционально-интегрирующий ФНЧ₁ обеспечивает устойчивость петли на переменном токе. Режекторный фильтр (РФ) и ФНЧ₂ подавляют f_φ и её гармоники на выходе ФД. Полосовой фильтр (ПФ) подавляет колебания суммарной и комбинационных частот. Отметим недостаток, что при f_φ≈10кГц. полоса пропускания петли ФАПЧ всегда меньше f_φ.и не обеспечивает требуемую часто высокую скорость перестройки СЧ.

Линеаризованную эквивалентную схему петли цифровой ФАПЧ c ФД типа «выборка с запоминанием» можно представить в виде (рис.4.10).

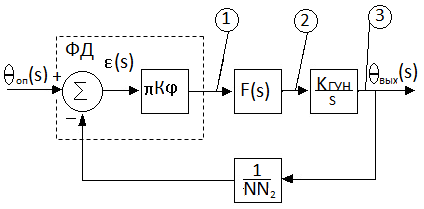
Рис.4.10. Линеаризованная эквивалентная схема петли

цифровой ФАПЧ c ФД типа «выборка с запоминанием» .

Эта схема отличается от такой же схемы петли аналоговой ФАПЧ (рис.4.4) коэффициентом обратной связи 1/N₂N и коэффициентом передачи ФД в виде πК _φ.

В цифровой ФАПЧ по аналогии с аналоговой:

- коэффициент передачи в прямом направлении равен

πК _φК_ГУН F(s)/s;

- коэффициент передачи разомкнутой цепи равен

(πК _φК_ГУН / N₂N) F(s) / s.

Введем обозначения:

α_φ= πК _φ ; α_ГУН=К_ГУН/NN₂. (4.47)

С учетом этих обозначений:

- коэффициент передачи в прямом направлении равен:

NN₂ (α_φ∙α_ГУН F(s) / s);

- коэффициент передачи разомкнутой петли равен:

α_φ α_ГУН F(s)/ s.

Отличие их от аналоговой ФАПЧ только в множителе NN₂ , который является cоnst относительно оператора Лапласа.

Поэтому для петли цифровой ФАПЧ можно построить аналогичную аналоговой модель петли рис.4.11 с параметрами, отнесенными к частоте ФД f_φ (т.е. множитель 1/NN₂ ввели в α_ГУН ).

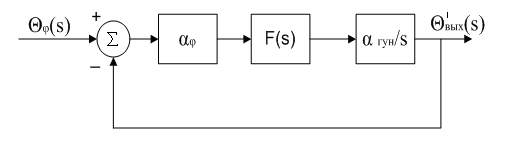
Рис.4.11. Линеаризованная эквивалентная схема петли цифровой ФАПЧ.

а) Петля цифровой ФАПЧ первого порядка.

При F(s)=1 коэффициенты передачи в прямом направлении и разомкнутой петли, отнесенные к f_φ равны

α_φ α_ГУН / s, (4.48)

а эквивалентная (4.9) функция передачи системы относительно f_φ равна:

. (4.49)

Отметим, что для получения параметров пели относительно частоты ГУН f_вых достаточно умножить выражения (4.48), (4.49) на N∙N₂.

Фазовая ошибка по аналогии с (4.11) равна

ε(s)= s∙θ_φ(s)/[s+ α_φ α_ГУН)] (4.50)

Согласно этому выражению и (4.4) фазовая ошибка в установившемся режиме петли ФАПЧ первого порядка (аналогичная (4.13 - 4.15)) равна (в радианах):

- при скачке фазы ОГ ∆θ_φ или ГУН ∆θ_вых

; (4.51)

- при скачке частоты ОГ Δω_φ или ГУН на Δω_вых

; (4.52)

-при линейном изменении входной частоты петли dΔω_φ /dt

.

Полоса пропускания (4.16) цифровой ФАПЧ первого порядка

В_3дБ= α_φ∙ α_ГУН/2π = f_ср [Гц] (4.53)

зависит от N на основании (4.47) в отличие от ФАПЧ 2^го порядка, для которой эта зависимость .

Шумовая полоса цифровой ФАПЧ первого порядка

В_Ш=α _φ∙α _ГУН/4 . (4.54)

Полоса удержания (4.25):

- отнесенная к частоте f_φ равна

[Δω_уд.]_φ=α_φ∙α_ГУН ; (4.55)

- отнесенная к частоте ГУН (т.к. Δω_φ= Δω_вых / NN₂) равна

[Δω_уд.]_вых= α_φ К_ГУН. (4.55′)

При этом полоса захвата равна полосе удержания.

Время захвата (4.26) по фазе при условии Δω < Δω_з равно:

. (4.56)

Несмотря на устойчивость петли ФАПЧ первого порядка, на практике она нуждается в компенсации устойчивости на переменном токе. Поэтому в эквивалентную схему петли цифровой ФАПЧ (в выражение фазового набега разомкнутой петли) включают фазовую задержку в ФД и цифровом делителе частоты рис.4.12.

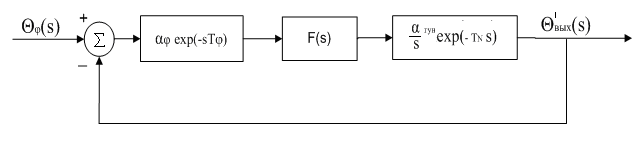
Рис.4.12. Линеаризованная эквивалентная схема петли цифровой

ФАПЧ с учетом фазового набега в ФД и делителе частоты.

Коэффициент передачи ФД типа «выборка-запоминание» можно упростить в виде:

G_φ(s) = α_φ [1 exp( sT_φ)] /s ≈ α_φ∙exp( sT_φ )_, (4.57)

если вслед за ФД установлены ФНЧ с достаточным подавлением частоты f_φ и ее гармоник, где T_φ=1/f_φ -период выборки.

Коэффициент передачи для ДПКД с делением на N или делителя с фиксированным делением на N₂ равен:

G_Ni(s) = exp( sT_Ni) / N_i , (4.58)

где T_Ni - задержка по времени, вносимая делителем.

В синхронных делителях эта задержка меньше периода входной частоты и при больших N_i ею можно пренебречь. Однако, когда входная частота делителя на несколько порядков выше f_φ, то эту задержку надо учитывать при анализе устойчивости петли.

С учетом этих задержек, выражения для АЧХ и ФЧХ коэффициента передачи разомкнутой петли цифровой ФАПЧ имеют вид:

G_T(ω) = 20lg|α_φ∙α_ГУН /j ω| = 20lg(α_φ∙α_ГУН /ω) (4.59)

Θ_T(ω)=( π/2)+( T_φ∙ω)+( T_N ω)+( T_N2 ω) (4.60)

Поскольку петля ФАПЧ неустойчива при больших коэффициентах передачи, то (с учетом соотношения (4.47), т.е. α_ГУН) эта неустойчивость будет при наименьших значениях N.