Б) Не линеаризованная петля фапч первого порядка

Для не линеаризованной петли рис.4.4 известно, что:

- фазовая ошибка ε_уст при скачке частоты Δω определяется уравнением:

sinε_уст = Δω / К_φ∙К_ГУН = Δω / К(0); (4.18)

где ε(s) = θ_оп(s) - θ_вых(s) = φ = θ_оп - θ_гун.

- коэффициент передачи петли

θ_вых(s) /θ_оп(s) = К(0)F(s) / [s + К(0) F(s) соsε_уст ] , (4.19)

где функция . (4.20)

Для такой петли ФАПЧ первого порядка F(s))=1, при скачке Δω на входе:

- коэффициент передачи равен

θ_вых(s) /θ_оп(s) = К(0) /[s+ К(0) соs ε_уст ]; (4.21)

- шумовая полоса

В_Ш = К(0) /4 соs ε_уст, [Гц]; (4.22)

- полоса пропускания

В_3дБ = (К(0) /2π)∙ [Гц] (4.23)

Следовательно, шумовая полоса В_Ш и полоса пропускания В_3дБ в ФАПЧ с синусоидальным ФД зависят с учетом (4.20) от величины отстройки Δω частоты ГУН и изменяются от В_{3дБ мин}=К(0)/2π при Δω=0 до В_3дБмaкс=√2∙К(0)/2π при Δω=К(0) в (4.23).

Фазовая ошибка ФАПЧ с синусоидальным ФД, работающим в диапазоне разности фаз φ = ±1 рад, определяется из уравнения (4.18)

ε_уст = arc sin(Δω /К(0)). (4.24)

Т. к. согласно (4.9′) выходное напряжение ФД равно V_б(t) = Е_т sinφ, то согласно (4.9′')

φ = arc sin(V_б(t)/ Е_т) =. arc sin(±1), (4.24′)

где при φ = ±1 радиан согласно (4.9′′) V_б(t) = ± Е_т.

Следовательно, для такой петли согласно эквивалентности уравнений (4.24) и (4.24′) максимальная отстройка частоты ГУН, которая может быть скомпенсирована и определяет полосу удержания ФАПЧ, должна удовлетворять соотношению ε_уст ≤ φ, т. е.

Δω/К(0) ≤±1, откуда следует:

- Полоса удержания определяется коэффициентом усиления К(0) и равна.

Δω_уд ≤ К_φ∙К_ГУН, Δf_уд ≤ К_φ∙К_ГУН /2π (4.25)

-Полоса захвата при этом равна Δω_з = Δω_уд.

Отметим, что для уменьшения ошибки (4.24) необходимо увеличивать коэффициент передачи петли К(0)= К_φ∙К_ГУН или ужесточать требования к Δω отстройки частоты ГУН. Однако это увеличение коэффициента ограничено устойчивостью петли и повышением фазовых шумов СЧ согласно (4.22).

Время захвата по фазе в не линеаризованной петле ФАПЧ первого порядка (когда Δω меньше полосы захвата) равно:

(4.26)

где δ_з–заданное отклонение ошибки ε (в радианах) за время t_зф от ее значения ε_уст.

Несмотря на то, что рассмотренная (рис.4.4) петля ФАПЧ первого порядка устойчива при любых К(0), реальные петли ФАПЧ содержат смесители, полосовые фильтры, ФНЧ, умножители, делители. В этом случае петля ФАПЧ может быть неустойчива.

Далее покажем, что применение пассивного пропорционально-интегрирующего фильтра в ФАПЧ позволяет увеличить К(0), т.е. уменьшить ошибку ε_уст , и обеспечить устойчивость петли на переменном токе.

С) Петля фапч второго порядка типа 1 с пассивным пропорционально - интегрирующим фильтром.

Функция передачи этого фильтра (рис.4.6) равна

F(s) = (1+τ₂s) /(1+τ₁s), (4.27)

где τ₁=(R₁+R₂)C; τ₂=R₂C.

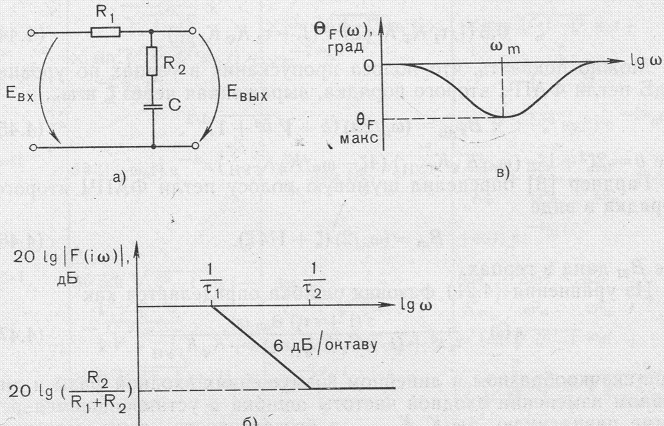
Рис.4.6. Схема и характеристики ФЧХ и АЧХ пассивного

пропорционально - интегрирующего фильтра.

Коэффициент передачи разомкнутой петли и на постоянном токе равен:

.

Эту систему относят к типу 1 с характеристиками рассмотренной петли первого порядка в установившемся режиме .

Однако, функция передачи петли ФАПЧ (4.9) с таким фильтром равна:

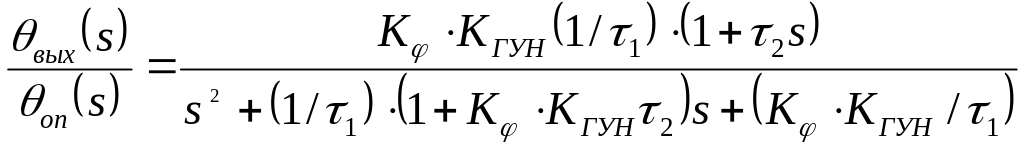(4.28)

и соответствует петле ФАПЧ второго порядка, т. к. наибольшая степень s в знаменателе равна 2.

Аналогично уравнению (4.11) фазовая ошибка равна

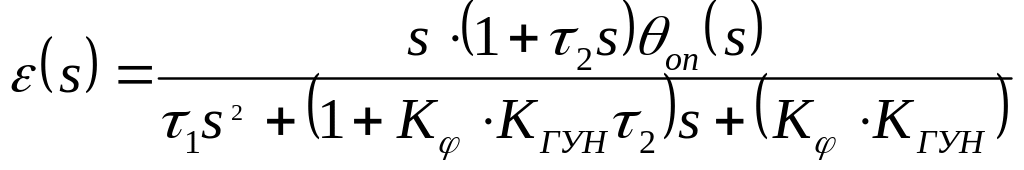(4.29)

Следовательно, как и для всех систем типа 1, входному скачку фазы, линейному изменению фазы и линейному изменению входной частоты установившееся значение фазовой ошибки равно соответственно нулю, Δω/К_φ∙К_ГУН и бесконечности. При этом, переходный процесс установления ε(t) зависит от параметров петли и F(s), т.е. как будет показано далее от коэффициент затухания петли η .

Известно, что для такой петли максимальное значение скорости изменения частоты ОГ (без срыва режима захвата) равно

(d Δω /dt)_оп ≤ ω²_п = ( К_φ∙К_ГУН /τ₁), (4.30)

где ω_n -собственная частота петли.

Соответственно, максимальная скорость изменения частоты ГУН для надежного захвата равна

(d Δω /dt)_ГУН ≤ ω²_п /2 (4.31)

или скорость изменения управляющего напряжения ГУН

│dЕ/dt │_макс ≤ ω²_п /2К_ГУН, (4.32)

т.к. d Δω/dt = К_ГУН│dЕ/dt │.

Полоса удержания петли второго порядка, как и в (4.25) равна

Δω_уд = К_φ∙К_ГУН,

а полоса захвата уменьшается и равна

Δω_з ≤ К_φ∙К_ГУН (τ₂/τ₁) , т.к. τ₂ < τ₁ . (4.33)

Шумовая полоса петли равна

В_ш = (ω_п / 2)( η+1 /4η), (4.34)

где коэффициент затухания петли

η = 0,5(1 / τ₁ К_φ∙К_ГУН)^1/2∙ (1+τ₂К_φ∙К_ГУН).

Графики зависимости ошибки (4.29) ε(t) во время переходного процесса при скачке фазы Δθ и различных значениях η даны на рис.4.7.

Рис. 4.7. Графики зависимости ошибки ε(t) во время переходного процесса

при скачке фазы Δθ и различных значениях коэффициента затухания η.

Время захвата фазы t_з.ф при начальной отстройке Δω ≤ Δω_з определяется выражением (4.26).

Время захвата частоты при отстройке Δω_з ≤ Δω ≤ Δω_зат равно (в секундах, с пропуском некоторых периодов ГУН):

t_{з.ч .}≈ 4(∆f)²/В_ш³, (4.35)

где ∆f = Δω /2π;

Δω_зат - затягивание частоты, т.е. предельное значение частоты отстройки

∆ω_зат ≈ √2 [2η ω_п∙К_φ∙К_ГУН∙F(s=0)  ω_n² ]^1/2 , (4.36)

которое справедливо при ω_n∙ К(0)∙F(0) ≤ 0,4.

Полное время захвата по фазе и частоте равно: t_{з. =} t_з.ч+ t_з.ф.

d) Петля ФАПЧ второго порядка типа 2 с идеальным интегратором.

В рассматриваемых ранее петлях ФАПЧ типа 1 не реализуется захват по фазе. При этом фаза выходного колебания СЧ зависит от отстройки ГУН (температурных воздействий) несмотря на постоянство фазы опорного колебания, т.е. фазовые соотношения между этими колебаниями используются для захвата частоты (отрабатываются с ошибкой 0 только скачки по частоте Δω). Для истинной петли ФАПЧ фильтр должен иметь функцию передачи идеального интегратора:

F(s) = (s+c) /s.

Приближенная реализация такой функции равна

(4.37)

и представлена на рис.4.8, где τ₂ = R₂С.

Рис.4.8. Схема и характеристики ФЧХ и АЧХ ФНЧ с

приближенной функцией передачи идеального интегратора.

Коэффициенты передачи разомкнутой петли и коэффициент передачи в прямом направлении равен

К_φ∙К_ГУН∙(R₂ /R₁)∙( s+1/τ₂) / s² (4.38)

и относит систему к типу 2.

Эта петля обеспечивает захват по фазе и отслеживает линейные изменения входной опорной частоты (частоты ГУН) в бесконечной полосе захвата, но с большим временем захвата.

Функция передачи петли ФАПЧ с идеальным интегратором согласно (4.9)

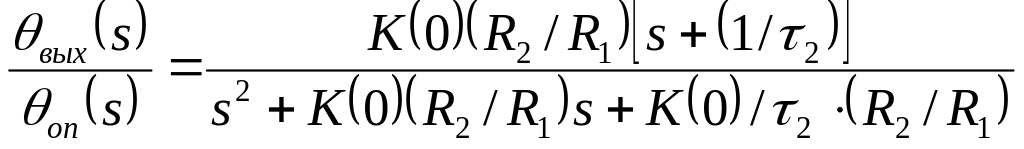. (4.39)

Ошибка фазы в соответствии с (4.11) равна

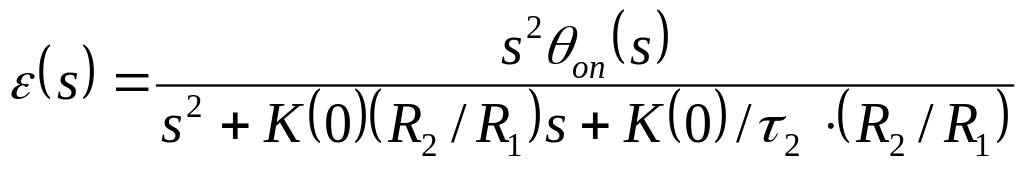. (4.40)

При линейном изменении входной частоты [θ_on(s)=(dΔω/dt)/s³] установившаяся ошибка равна

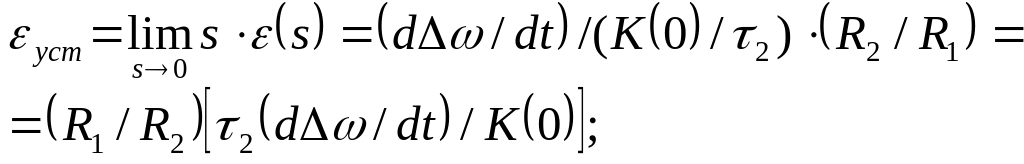(4.41)

При нелинейном синусоидальном ФД с полосой ±1рад эта ошибка

ε_уст = arcsin[(R₁/R₂) τ₂ (dΔω /dt) /K(0)], а (4.42)

φ = arc sin(V_б(t)/ Е_т) =. arc sin(±1),

откуда ограничение на скорость изменения частоты ОГ для условия обеспечения захвата ε_уст ≤ φ по аналогии с (4.24)-(4.25) равно:

(dΔω /dt)_оп ≤ (R₂ / R₁)∙K(0) / τ_{2 .} (4.43)

Аналогично, ограничение:

- на скорость изменения частоты ГУН

(dΔω/dt)_ГУН ≤ (1/2τ₂)∙K(0)(R₂/R₁),∙ (4.44)

-на скорость изменения управляющего напряжения ГУН

│dЕ/dt │_мак = (1/2К_ГУН ∙ τ₂) ∙K(0)(R₂ / R₁).∙ (4.45)

т.к. (dΔω/dt)_ГУН = К_ГУН ·│dЕ/dt │

Известно также, что полоса затягивания частоты Δω_зат при отстройке Δω >Δω_з в петле ФАПЧ с идеальным интегратором бесконечна, а время захвата увеличивается с увеличением первоначальной отстройки ГУН Δω и равно

t_з.ч.=τ₂ [Δω / K(0)(R₂ /R₁)  sinθ₀ ] (4.46)

где θ₀ - начальный сдвиг фаз (в радианах) между колебаниями ОГ и ГУН.