
4. ПЕТЛИ ФАПЧ СИНТЕЗАТОРОВ ЧАСТОТ
Рассмотрим петли ФАПЧ применительно к СЧ с точки зрения получения заданного шага сетки частот, оптимизации фазовых шумов, подавления побочных составляющих в выходном колебании СЧ и повышения скорости переключения частоты.
4.1. Петля ФАПЧ - как система регулирования с обратной связью
представлена на рис.4.1:
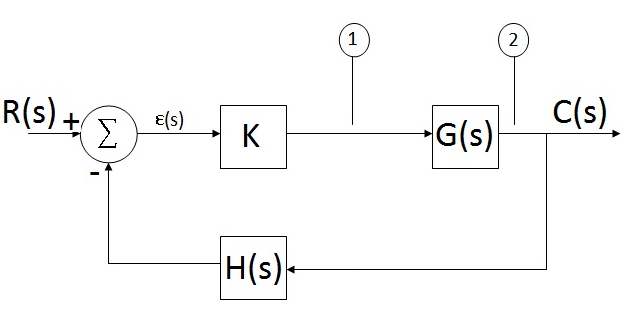
Рис.4.1. Петля ФАПЧ - как система регулирования с обратной связью.
где K∙G(s) – коэффициент передачи в прямом направлении;
K∙G(s)∙H(s) – коэффициент передачи разомкнутой петли;
s- переменная преобразования Лапласа (комплексная частота, s = α+јω).
Сигнал ошибки в системе регулирования равен
(s) =R(s) C(s)H(s),
а сигнал на выходе системы равен
C(s)= (s)KG(s) = R(s)KG(s) C(s)H(s)KG(s) или (4.1′)
C(s)(1+ H(s)KG(s) ) = R(s)KG(s). (4.1'′)
Коэффициент передачи системы (реакция системы на изменение s колебания опорной частоты R(s) ) :
![]() , (4.1)
, (4.1)
т.е. отношению коэффициента передачи (от точки возмущения до выхода) в прямом направлении к 1 плюс коэффициент передачи разомкнутой петли.
Коэффициент передачи системы от точки 1, 2 до выхода, соответственно, равен:
![]() ;
; ![]() . (4.2)
. (4.2)
Сигнал ошибки (s) системы на входное возмущение R(s) найдем из уравнения (4.1′) , выражая KG(s) из (4.1'′):
![]() . (4.3)
. (4.3)
Ошибка εуст устойчивой системы регулирования в установившемся режиме (полюса в левой полуплоскости) по теореме о конечных приращениях равна:
![]() , (4.4)
, (4.4)
где R(s) преобразование Лапласа входных функций возмущения согласно таблице № 4.1:
Таблица № 4.1
-
Функция
r(t)
R(s)
Преобразование Лапласа
Ступенчатая
Линейная
Параболическая
А
vt
0,5 at2
A/s (
 )
)v/s2
a/s3
Таким образом, ошибка εуст (4.4) в установившемся режиме определяется видом функции R(s) возмущений на входе системы и коэффициентом передачи разомкнутой петли K∙G(s)∙H(s) , который может быть представлен отношением полиномов.
Тип системы определяет значение п показателя степени при s в факторизованном знаменателе коэффициента передачи K∙G(s)∙H(s):
так п=0 - соответствует системе типа «0», а п=1 - системе типа «1» и т.д.
Порядок системы определяется наибольшим значением п показателя степени при s в знаменателе коэффициента передачи системы (4.1).
Однако, уменьшение ошибки εуст за счет увеличения коэффициента K∙G(s)H(s) приводит к неустойчивости системы.
Система неустойчива на частоте, например ω1, соответствующей сдвигу фазы на ±180°, если коэффициент передачи разомкнутой петли K∙G(s)∙H(s) на этой частоте превышает единицу, т.е
. 20lg│KG(jω1)H(jω1)│> 0
Характеристики устойчивости системы определяют по диаграмме Боде рис.4.2 .
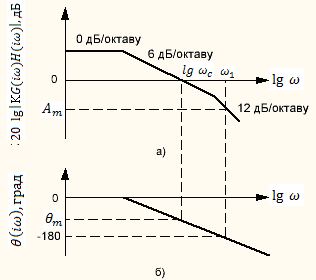
Рис.4.2. Диаграмма Боде устойчивости системы регулирования.
Запас устойчивости по усилению определяется величиной
Ат= 20lg│KG(jω1)H(jω1)│. (4.5)
Запас устойчивости по фазе (в градусах) определяется величиной
θт=180°+θ(jωс), (4.6)
где ωс -частота, при которой коэффициента передачи разомкнутой петли равен 1;
θ(jωс) – сдвиг фазы в системе с разомкнутой петлей обратной связи.
Для устойчивой системы необходим запас: Ат ≥ 10дБ и θт ≥ 30°.
Шумовая полоса системы регулирования определяется АЧХ коэффициента передачи (4.1), в герцах (полоса эквивалентной прямоугольной АЧХ ФНЧ ):
![]() . (4.7)
. (4.7)
Ширина полосы пропускания системы характеризует инерционность системы и определяется по уровню половинной мощности АЧХ
В3дБ =│С(jω)/R(jω)│2 3дБ = (0,707)2 (4.8)
4.2. Петли аналоговой фапч сч.
В отличие от петли ФАПЧ ЧМ приемника (следящего фильтра с узкой шумовой полосой) в СЧ на основе ФАПЧ эта полоса достаточно широкая, регулируемая из соображений минимума фазовых шумов СЧ.
Оценим характеристики полосы захвата, удержания, время переключения СЧ на основе петли ФАПЧ первого и второго порядка, структурная схема которой представлена на рис. 4.3,
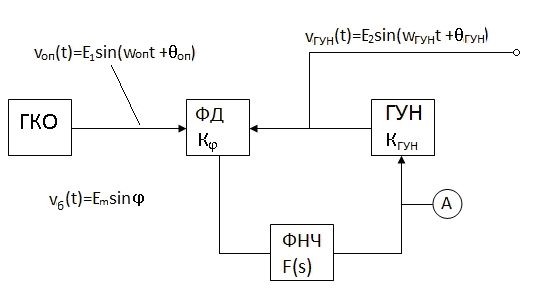
Рис.4.3. Структурная схема СЧ на основе петли ФАПЧ.
где КГУН – крутизна электронной настройки ГУН в [рад /В∙с];
Кφ – крутизна характеристики фазового дискриминатора в [В/рад]:

Рис.4.3'. Характеристика фазового дискриминатора.
где φ=θоп - θгун - в радианах;
напряжение биений:
Vб(t)=Emsin(φ=θоп - θгун). (4.9′)
При замкнутой петле φ →0 и sin(φ) = φ , а максимум напряжения биений в вольтах:
Vб(t)=Ет·[половина полосы ФД(φ=θоп-θгун)] .
Для синусоидального ФД с рабочей полосой φ=±1 рад этот максимум равен
Ет= Vб(t) /φ = Кφ = Ет /1. (4.9′′)
Эквивалентная схема петли ФАПЧ, как системы регулирования, учитывающая нелинейность синусоидального ФД, приведена на рис.4.4, где ε(s) = φ = θоп(s ) - θгун(s)

Рис.4.4. Эквивалентная схема нелинейной петли ФАПЧ.
При линейном ФД в диапазоне значений φ либо при малой величине ошибки в установившемся режиме ФАПЧ (т.е. соsεуст=1) получим линеаризованную эквивалентную петлю ФАПЧ.
Для линеаризованной петли можно определить, по аналогии с обобщенной системой регулирования (рис.4.1):
- коэффициент передачи системы (4.1)
![]() ,
(4.9)
,
(4.9)
который является ФНЧ по отношению к шумам ОГ, т.е. θвых(s)/θоп(s)→1 при s→0 и к нулю при s→∞;
- коэффициент передачи системы от точки 3 до выхода аналогично (4.2)
1/[1+ Кφ КГУНF(s)/s] , (4.10)
который определяет коэффициент передачи петли как ФВЧ по отношению к шумам ГУН, т.е. θвых(s)/θгун ш→0 при s→0.
-фазовая ошибка аналогично (4.3) равна
ε(s)=θоп(s) - θвых(s) = s∙θоп(s) /[s+ Кφ КГУНF(s)] (4.11)
Далее проведем анализ аналоговых петель ФАПЧ различного порядка.
А) Петля фапч первого порядка (линеаризованная)
имеет место при отсутствии фильтра F(s)=1, т.к. порядок степени s в знаменателе (4.9) равен 1. Система относится к типу 1 по причине равенства п=1 показателя знаменателя коэффициента передачи разомкнутой петли, равного при отсутствии фильтра коэффициенту в прямом направлении K∙G(s)=Кφ∙КГУН /s, где числитель определяет коэффициент передачи на постоянном токе
К (s = 0) = Кφ∙КГУН. (4.12)
Определим ошибку εуст (4.4) петли в установившемся режиме для различных входных возмущений согласно таблице 4.1.
Фазовая ошибка в установившемся режиме системы согласно (4.4):
-при скачке фазы Δθоп на входе т.е. [θоп(s)= Δθоп/s] равна нулю
![]() (4.13)
(4.13)
- при линейном возмущении фазы или скачке опорной частоты на величину Δω, т.е. при .[θоп(s)= Δω/s2 ] равна const
![]() , (4.14)
, (4.14)
т. е., петля первого порядка компенсирует любые скачки фазы на входе в пределах полосы удержания петли и следит за скачками частоты с ошибкой по фазе, которая пропорциональна величине скачка Δω и обратно пропорциональна коэффициенту передачи на постоянном токе (4.12) К (s = 0).
- при линейно изменяющейся частоте dΔω/dt [рад/сек] т.е. при [θоп(s)=dΔω/dt/ s3] равна
![]() (4.15)
(4.15)
Это означает, что превышение определенного значения скорости изменения частоты ОГ (или ГУН) приведет к нарушению режима захвата.
На рис.4.5 приведены графики ошибки (4.13)÷(4.15) во временном масштабе для системы первого порядка.
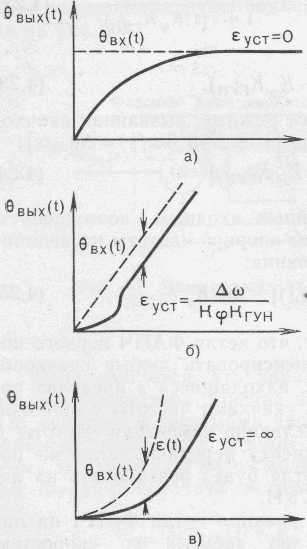
Рис.4.5. Графики ошибки εуст во временном масштабе для
системы первого порядка при возмущениях согласно таблице 4.1 .
Постоянная времени установления ошибки фазы определяется шириной полосы пропускания (4.8) ФАПЧ по уровню 3дБ с учетом (4.9):
В3дБ =Кφ∙КГУН /2π = fср [Гц] (4.16)
(![]() )
)
т. е. быстрая реакция петли (более широкая полоса) обеспечивается увеличением коэффициентом передачи К (s = 0)=Кφ∙КГУН.
Кроме того, ширина полосы пропускания В3дБ важна для оптимизации фазовых шумов ФАПЧ, т.к. согласно (4.9) система ведет себя по отношению к шумам частоты ОГ как ФНЧ с подавлением за полосой 6дБ/октаву и как ФВЧ согласно (4.10) по отношению к шумам ГУН.
Шумовая полоса линеаризованной ФАПЧ первого порядка равна
ВШ=Кφ∙КГУН/4 [Гц]. (4.17)
