Тема 3. Другий закон термодинаміки

Самочинні та не самочинні процеси. Формулювання другого закону термодинаміки і його аналітичний вираз. Розрахунок зміни ентропії у різних процесах. Статистичний характер другого закону термодинаміки. Термодинамічна вірогідність. Ентропія як міра вірогідності. Формула Больцмана. Абсолютні значення ентропії. Постулат Планка. Третій закон термодинаміки. Залежність ентропії від температури. Функції Гіббса і Гельмгольца як критерій напряму процесу

Перший принцип термодинаміки стверджує еквівалентність різ­них форм енергії і дає кількісні співвідношення, справедливі при будь-яких переходах. Але він не дає ніяких відомостей про на­прям, в якому відбувається перехід насправді.

Наприклад, якщо система цинк — сірчана кислота, що знахо­диться у певному стані, будь-яким шляхом переходить у новий певний стан сульфат цинку — водень, то згідно з першим законом загальна кількість теплоти і роботи залишається незмінною. Крім того, при зворотному переході загальний енергетичний баланс буде тим же, але з протилежним знаком. Однак з досвіду відомо, що цинк самочинно реагує із сірчаною кислотою, у той час як зворо­тний перехід вимагає втручання ззовні, витрати роботи.

Таким чином, всі процеси можуть бути поділені на дві групи: процеси самочинні, або спонтанні (позитивні), які проходять самі по собі, і процеси не самочинні (негативні), які вимагають для свого проходження витрати роботи.

Самочинні процеси проходять у напрямі наближення системи до рівноважного стану. Ідеальним граничним випадком процесів, які лежать між самочинними і не самочинними, є рівноважні процеси, при яких відбувається перехід системи у прямому або зворотному напрямі через послі­довність рівноважних станів.

Другий закон термодинаміки дає можливість передбачити на­прям перебігу процесу в заданих умовах, а також характеризувати рівноважний стан системи.

Другий закон (принцип) термодинаміки, як і перший, є посту­латом, який неможливо довести на основі інших положень. Неможливий самочинний перехід теплоти від менш нагрітого тіла до більш нагрітого. Отже, неможливо сконструювати машину, яка б у круговому процесі тільки переносила тепло від більш холодного тіла до більш нагрітого.

Інше формулювання запропоноване В. Томсоном (лордом Кель­віном, 1851):

Неможливо побудувати періодично діючу машину, яка б тільки одержувала тепло від теплового резервуару і повністю перетворюва­ла його в еквівалентну кількість роботи (принцип неможливості вічного двигуна другого роду).

З другого закону термодинаміки випливає, що люба форма енергії – механічна, електрична, хімічна – може повністю переходити в тепло, однак зворотній повний перехід не можливий, тому що частина теплової енергії розсіюється. Для характеристики незворотності енергетичних переходів при різних фізичних і хімічних процесах застосовується особа величина – ентропія S, як та частина енергії, яка не перетворюється у корисну роботу. Зміна ентропії при оборотному процесі визначається рівнянням(оскільки ):

= .

В цьому рівнянні С – теплоємкість при постійному тиску Ср, або постійному об’ємі Сv.

Для не оборотних процесів . Таким чином, зміни ентропії в ізольованій системі вказують на можливість самочинних переходів у системі(збільшення ентропії), або на стан рівноваги(сталість ентропії).

Можна сказати що ентропія є мірою невпорядкованості стану системи. Системи прагнуть перейти з більш впорядкованого стану до менш впорядкованого стану, який характеризується збільшенням ентропії.

Виходячи із рівняння можна розрахувати зміну ентропії у різних процесах:

1.для ізотермічного процесу(при переході речовини з одного агрегатного стану у інше):

.

Для процесу плавлення q – теплота плавлення і т.д.

2.Змішання двох ідеальних газів при сталих температурі і тиску:

.

3.Нагрівання при сталому об’єму або тиску:

.

Стан системи можна характеризувати мікро станами часток, які її складають – їх миттєвими координатами і швидкостями різних видів руху у різних напрямках. Число мікро станів системи зветься термодинамічною вірогідністю системи W. Оскільки число часток у системі значне, імовірність виражається значними числами. Тому користуються логарифмом термодинамічної вірогідності, який зв’язане з ентропією формулою Больцмана: S = кlnW і є ентропією системи. Множник к дорівнює сталій Больцмана. Статистичний характер другого закону термодинаміки вказує на те, що збільшення ентропії відображає найбільш вірогідний шлях змін.

Розглянуті вище співвідношення дають можливість розрахува­ти тільки зміни ентропії, але не дозволяють знайти її абсолютне значення. Ентропію можна обчислити на основі постулату План­ка (1912), згідно з яким ентропія ідеального кристала індивідуальної речовини дорівнює нулю при абсолютному нулі температури S₀ = 0. Цей постулат називають також третім законом термодинаміки.

Зі збільшенням температури зростає швидкість різних видів руху часток, а відповідно і число їх мікро станів і термодинамічна імовірність і ентропія. При переході речовини з твердого стану у рідкий значно збільшується невпорядкованість і ентропія речовини. Особливо різко збільшується ентропія при переході з рідкого у газоподібний стан. Збільшення числа атомів у молекулі і ускладнення молекули призводять до збільшення ентропії. Можна розрахувати зміну ентропії хімічної реакції яка дорівнює різниці(з урахуванням стехіометричних коефіцієнтів) між сумою ентропій продуктів реакції і сумою ентропій вихідних речовин.

У довідкових таблицях термодинамічних властивостей речовин звичайно наводяться величини S — стандартні ентропії при 298 К і р = 1,013 10⁵ Па. Для знаходження абсолютних ентропій в інших умовах необхідно до цих значень додати зміни, пов'язані з перехо­дом із стандартного стану в новий.

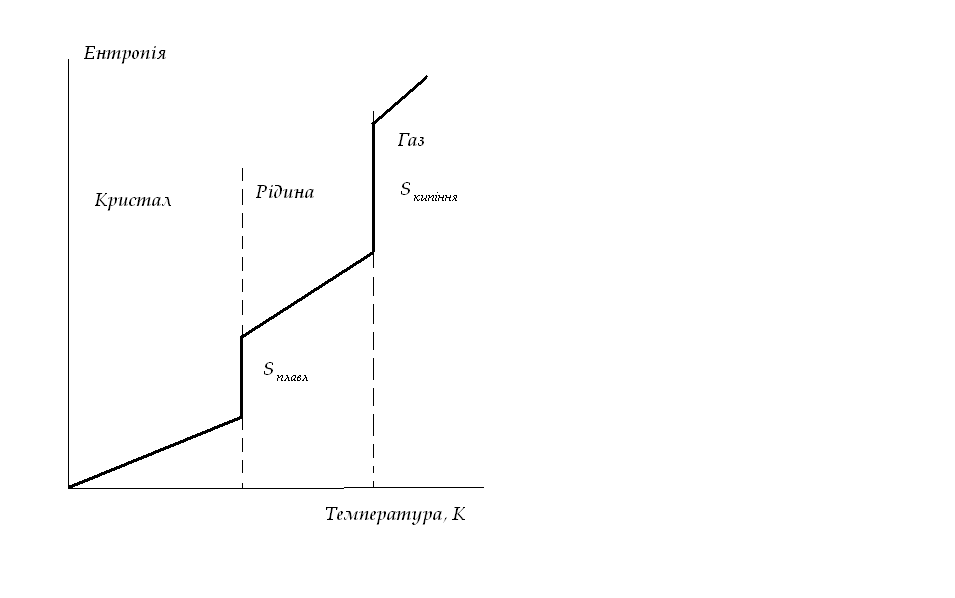
Рисунок. Зміна ентропії речовини зі збільшенням температури.

Таким чином для систем, які не обмінюються з зовнішнім середовищем ні енергією ні речовиною другий закон термодинаміки можна сформулювати наступним чином: в ізольованих системах самочинно йдуть тільки такі процеси, які супроводжуються зростанням ентропії.

Однак, системи, в яких перебігають хімічні реакції не ізольовані, тому що вони супроводжуються зміною внутрішньої енергії(тепловим ефектом реакції), обмінюються енергією з зовнішнім середовищем і таким чином зазвичай супроводжуються як зміною ентропії, так і зміною ентальпії. В хімічних процесах проявляються дві протилежні тенденції: а) прагнення до утворення міцних зв’язків між частками, виникнення більш складних речовин, що супроводжується зменшенням енергії системи(ентальпійний фактор - ); б) прагнення до роз’єднанню часток, до безладдя, що характеризується збільшенням ентропії(ентропійний фактор -Т ). Кожний з зих факторів окремо не може бути критерієм самочинності хімічної реакції. Для ізобаро-ізотермічного процесу їх об’єднує термодинамічна функція, яка зветься енергією Гіббса( ):

.

Це рівняння можна записати у вигляді:

.

Ентальпія хімічної реакції складається з двох частин. Перша ( ) дорівнює максимальній роботі А_max, яку може виконати система, або частина енергетичного ефекту хімічної реакції, яку можна перетворити в роботу: А_max, або її ще називають вільною енергією. Друга частина(ентропійний фактор) – це частина енергетичного ефекту, яку не можливо перетворити на роботу, вона розсіюється у зовнішнє середовище у вигляді теплоти і ентропійний фактор зветься зв’язаною енергією. Енергія Гіббса є критерій самочинності перебігання хімічної реакції при ізобаро-ізотермічних процесах. Хімічна реакція принципово можлива коли . Якщо , хімічна реакція не може перебігати самочинно. Якщо , реакція зворотна і може перебігати як у прямому, так і у зворотному напрямках.

Напрямок реакції залежить від її характеру. Якщо реакція екзотермічна( ) і в результаті реакції збільшується число моль газоподібних речовин( ), то вона перебігає у прямому напрямку при любих температурах. Навпаки, якщо і зменшується число моль газоподібних речовин , реакція не може перебігати самочинно у прямому напрямку при любій температурі.

Якщо , і самочинно може перебігати пряма реакція при низьких температурах Т Т_р= і зворотна при високих.

Якщо , і самочинно може перебігати пряма реакція при високих температурах Т Т_р= і зворотна при низьких.

В довідниках наведені стандартні значення зміни енергії Гіббса при утворенні 1 моль речовини з простих речовин, стійких при 298 К(енергі Гіббса утворення речовини - ). Енергію Гіббса хімічної реакції можна розрахувати як різницю між сумою енергій Гіббса утворення продуктів реакції і сумою енергій Гіббса утворення вихідних речовин з урахуванням стехіометричних коефіцієнтів. Отримане значення зветься стандартною енергією Гіббса хімічної реакції і є критерієм самочинного перебігання реакції при стандартних станах вихідних речовин і продуктів реакції.

Для ізохоро-ізотермічних умов максимальна робота системи при рівноважному проведенню процесу дорівнює зміні енергії Гельмгольца :

.

Енергія Гельмгольца характеризує напрямок самочинного перебігання хімічної реакції при ізохоро-ізотермічних умовах, що можливо, коли .

Зв’язок розглянутих термодинамічних функцій між собою наведено на рисунку.

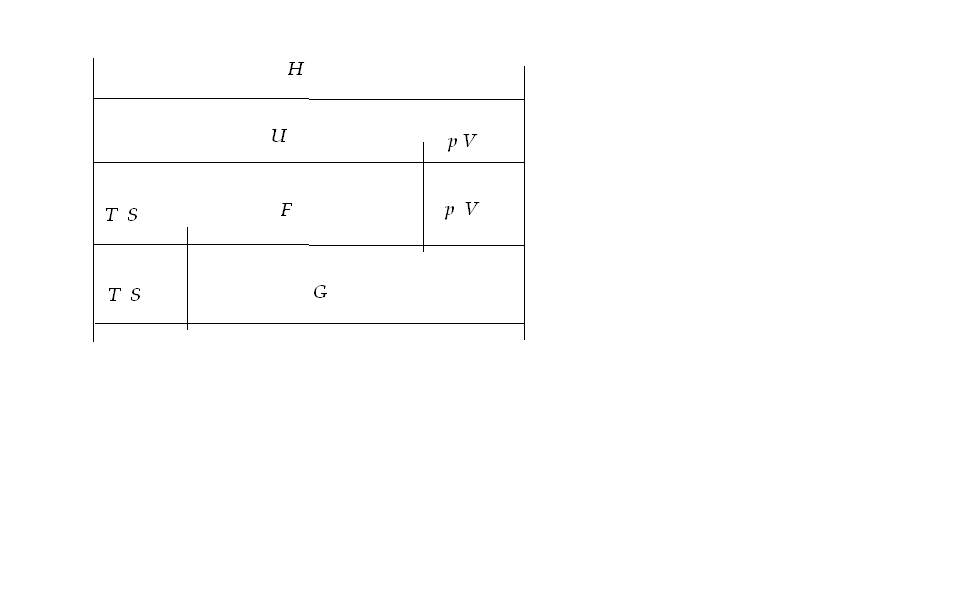
Рисунок. Зв’язок термодинамічних функцій між собою.